Moteurs à courant continu
Les moteurs à courant continu sont des appareils qui transforment l'énergie électrique qu'ils reçoivent en énergie mécanique. La construction des moteurs est identique à celle des génératrices, de sorte qu'une machine à courant continu peut servir indifféremment comme moteur ou comme génératrice. L'usage des moteurs à courant continu est plutôt restreint, car la distribution se fait à courant alternatif.
Cependant, pour certaines applications il est parfois avantageux d'utiliser des moteurs à courant continu alimentés par des convertisseurs qui transforment le courant alternatif en courant continu. La supériorité de ces moteurs réside dans le fait qu'ils se prêtent facilement à un contrôle souple, continu et presque instantané de leur vitesse. Les moteurs à courant continu ont les mêmes modes d'excitation que les génératrices.
On distingue donc:
1. les moteurs à excitation shunt
2. les moteurs à excitation série
3. les moteurs à excitation compound
De plus, tout comme pour les génératrices, la réaction d'induit se manifeste dans les moteurs, produisant une distorsion et un affaiblissement du flux provenant des pôles à mesure que la charge augmente.
Les problèmes de commutation existent également, c'est pourquoi les moteurs de puissance supérieure à 1 kW contiennent toujours des pôles de commutation. Dans le cas des génératrices, seuls la tension et le courant ont retenu notre attention.
Cependant, pour les moteurs, la compréhension des phénomènes mécaniques faisant intervenir le couple, la vitesse et l'inertie est particulièrement importante.
Nous encourageons donc le lecteur à revoir à la section Notions de mécanique les lois fondamentales reliant ces trois paramètres.
Force contre-électromotrice
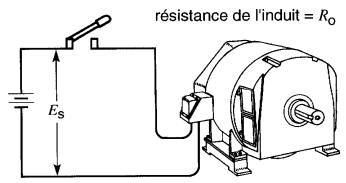
Considérons une machine bipolaire dont l'inducteur est un aimant permanent, et dont l'induit, de résistance Ro, est raccordé à une source de tension ES (Fig. 28-1).
Figure 28-1 Démarrage d'un moteur à courant continu

Avant que l'interrupteur ne soit fermé, l'induit est immobile. Dès qu'il est fermé, la source fait passer un courant très intense dans l'induit, car la résistance Ro de celui-ci est très faible (Fig. 28-2).
Figure 28-2 La rotation du moteur induit une tenson Eo, appelée force contre-électromotrice
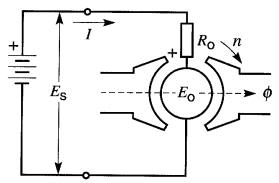
Or, nous savons (principe II de l'électromagnétisme) que le passage du courant dans les conducteurs de l'induit, situés dans le champ magnétique de l'aimant permanent, engendre une force sur chacun d'eux. L' action de ces forces produit un couple qui fait tourner l'induit.
D'autre part, dès que l'induit se met à tourner, un autre phénomène se manifeste: l'effet générateur. En effet, dans toute machine à courant continu, une tension est induite dans les conducteurs de l'induit dès que ceux-ci coupent des lignes de flux, quelle que soit la cause produisant le mouvement de l'induit.
La valeur et la polarité de la tension sont les mêmes que celles qu'on obtiendrait si la machine fonctionnait comme génératrice. Comme pour cette dernière, la tension induite Eo est proportionnelle à la vitesse de rotation n du moteur et au flux 0entre les pôles. Elle peut donc être exprimée par la même équation que celle utilisée pour les génératrices, soit :
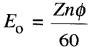 (28-1)
(28-1)
où
Eo
= tension induite dans l'induit [V]
Z = nombre de conducteurs sur l'induit
n = vitesse de rotation du moteur [r/min]
Φ = flux par pôle [Wb]
60 =
constante tenant compte des unités
Pour les moteurs, cette tension induite Eo porte le nom de force contre-électromotrice (f.c.é.m.) car sa polarité est telle qu'elle agit «contre» la tension de la source. Elle s'y oppose en ce sens que la tension totale agissant sur le circuit série de la Fig. 28-2 est égale à (Es - Eo) volts et non pas à (Es + Eo) volts.
Accélération du moteur
La tension résultante agissant sur le circuit valant (Es - Eo) volts, le courant I n'est limité que par la résistance Ro, ce qui donne:
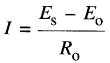 (28-2)
(28-2)
Lorsque le moteur est au repos, la vitesse est nulle, donc la tension induite Eo = 0, et l'équation ci-dessus devient:
I = Es / Ro
C'est dire qu'au démarrage le courant est énorme car la résistance Ro de l'induit est très basse.
En effet, ce courant de démarrage peut être de 20 à 50 fois plus grand que le courant de pleine charge du moteur. La grande force agissant alors sur les conducteurs produit un couple de démarrage puissant, provoquant une accélération rapide de l'induit.
À mesure que la vitesse croît, Eo augmente et la valeur de la tension résultante (Es - Eo) diminue.
On en conclut que le courant I diminue avec l'augmentation de la vitesse. Pendant que le courant diminue dans l'induit, le moteur continue d'accélérer jusqu'à une vitesse limite. Pour la marche à vide, cette vitesse est telle qu'elle produit une force contre-électromotrice légèrement inférieure à la tension de la source.
En effet, si la f.c.é.m. pouvait devenir égale à la tension de la source, la tension résultante (Es - Eo) serait nulle, ce qui donnerait une valeur nulle pour le courant I.
Dans ces conditions, aucune force électromagnétique n'agirait sur les conducteurs de l'induit. Cependant, pour continuer à tourner, le moteur doit toujours produire un couple suffisant pour vaincre le frottement. Par conséquent, la f.c.é.m. doit donc être quelque peu inférieure à la tension de la source pour permettre le passage du faible courant nécessaire à la production de ce couple.
Exemple 28-1
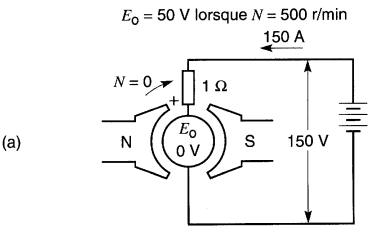
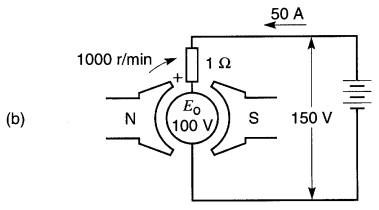
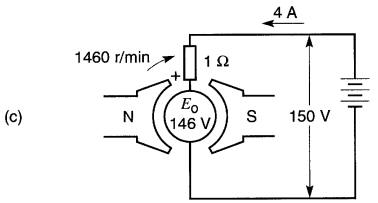
L'induit d'une machine bipolaire, dont la résistance est de 1Ω, génère une tension de 50V lorsque sa vitesse de rotation est 500 r/min. L'inducteur est composé de deux aimants permanents. L'induit est raccordé à une source de 150V (Fig. 28-3).
Figure 28-3
a. Conditions lorsque l'induit est au repos (voir exemple 28-1);
b. Conditions lorsque l'induit tourne à 1000 r/min;
c. Conditions lorsque l'induit tourne à 1460 r/min.
Calculer:
a) le courant de démarrage
b) la f.c.é.m. Eo lorsque le moteur tourne 1000 r/min : à 1460 r/min
c) le courant dans l'induit à 1000 r/min : à 1460 r/min
Solution
a) Au moment où le moteur démarre, l'induit ne tourne pas et, par conséquent, la tension induite Eo = 0 V (Fig. 28-3a). Le courant de démarrage étant seulement limité par la résistance de l'induit, sa valeur est:
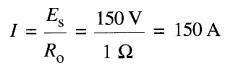
b) Étant donné que la tension induite à 500 r/min est de 50V, la f.c.é.m. du moteur à 1000 r/min sera 100V, et à 1460 r/min, 146V. Remarquer que la f.c.é.m. (ou tension induite) est proportionnelle à la vitesse.
c) La f.c.é.m. étant de 100V à 1000 r/min, il s'ensuit que la tension résultante dans le circuit de l'induit (Fig. 28-3b) est:
Es - Eo= 150 - 100 = 50V
Le courant dans l'induit vaut donc:
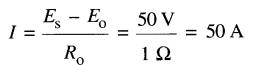
Lorsque le moteur atteint une vitesse de 1460 r/min (Fig. 28-3c) la f.c.é.m. sera 146V, soit une tension presque égale à la tension de la source. Dans ces circonstances, le courant dans l'induit n'est que :
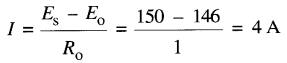
et le couple développé par le moteur est beaucoup plus petit qu'auparavant.
Expression du couple
La puissance mécanique et le couple sont deux des caractéristiques importantes d'un moteur à c.c. Nous décrivons ci-après les équations permettant d'évaluer ces deux grandeurs.
On a vu que la tension induite dans un enroulement imbriqué est donnée par:
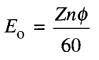 (28-1)
(28-1)
En se référant à la Fig. 28-2, la puissance électrique fournie à l'induit est:
Ps = EsI
D'autre part, Es est égale à la f.c.é.m. de EO plus la chute de tension ROI dans l'induit soit:
Es = EO + ROI
Par conséquent, la puissance fournie à l'induit est :
Le terme ROI² représente les pertes Joule dissipées sous forme de chaleur dans l'induit.
Par conséquent, le très important terme EOI représente la puissance électrique convertie en puissance mécanique.
Donc:
Pm = EOI (28-3)
où
Pm = puissance mécanique développée par le moteur [W]
EO = f.c.é.m du moteur [V]
I = courant dans l'induit [A]
Rappelons que la puissance mécanique d'une machine est donnée par:
Pm = nT19,55 (1-5)
où n est la vitesse de rotation en tours par minute et T le couple, en newton-mètre.
En combinant les équations (28-1), (28-3) et (1-5) on obtient:
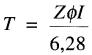
où
T = couple du moteur
[N•m]
Z = nombre de conducteurs sur l'induit = flux par pôle [Wb]
I = courant dans l'induit [A]
6,28 = constante tenant compte des unités [valeur exacte = 2π]
Cette équation indique qu'on peut augmenter le couple d'un moteur en augmentant, soit le courant I dans l'induit, soit le flux θ provenant des pôles.
Exemple 28-2
L'induit d'un moteur à c.c. de 225 kW, 250V, 1200 r/min contient 243 bobines et possède une résistance de 0,0094Ω.
L'enroulement est imbriqué et chaque bobine possède 1 spire (Fig. 28-4a et 28-4b).
L'inducteur comprend 6 pôles. Lors d'un essai sous charge, on prend les lectures suivantes: On considère que la chute de tension dans les balais est 1V.
Calculer:
a) le flux par pôle
b) la puissance mécanique développée par le moteur
c) le couple développé
Solution
a) La f.c.é.m est:
EO= Es - ROI - Echute dans les balais = 243 - 0,0094 x 638 - 1 = 243 - 6 - 1 = 236 V
le nombre de conducteurs sur l'induit est:
Z = 243 bobines x 2 conducteurs/bobine = 486
En utilisant l'équation 28-1, le flux par pôle est :
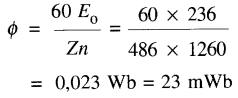
b) La puissance mécanique est :
Pm = EOI = 236V x 638A = 150,6 kW
c) Le couple du moteur est:
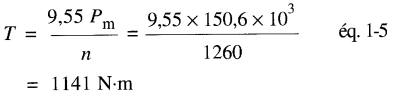
Figure 28-4a Noyau d'induit et collecteur d'un moteur de 225 kW, 250V, 1200 r/min. Le noyau de fer a un diamètre de 559 mm et une longueur de 235 mm ; il est composé de 400 tôles dentées de 0,56 mm.

Figure 28-4b Bobinage d'un induit de moteur à c.c. de 225 kW pour pelle mécanique. 1) machine-outil utilisée pour former les bobines ; 2) bobine formée prête à être introduite dans les encoches; 3) et 4) raccordement des bobines au collecteur de 243 lames

Expression de la vitesse
Lorsqu'un moteur à courant continu marche en régime normal, la chute de tension ROI dans la résistance de l'induit est généralement faible, de sorte qu'on peut la négliger dans la plupart des calculs de la vitesse. Cette approximation revient à supposer que la f.c.é.m. EO est égale à la tension de la source Es (Fig. 28-2).
D'autre part, nous avons vu que la f.c.é.m. peut s'exprimer sous la forme:
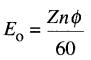
En remplaçant EO par Es , on obtient:
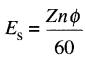
on en déduit que la vitesse est:
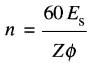 (approximativement)
(28-5)
(approximativement)
(28-5)
où
n = vitesse de
rotation [r/min]
Es = tension aux bornes de l'induit [V]
Z = nombre de conducteurs sur l'induit
θ = flux par pôle [Wb]
Pour un moteur donné, cette expression nous indique que la vitesse de rotation dépend de la tension de la source Es et du flux par pôle θ. Étudions d'abord l'effet de Es.
Réglage de la vitesse par la tension de l'induit
Si le flux 0 ne varie pas (cas d'un inducteur à aimant permanent, ou d'un inducteur à courant d'excitation constant), l'équation 28-5 nous indique que la vitesse ne dépend plus que du terme Es, c'est-à-dire de la tension de la source.
Si l'on augmente ou diminue Es, la vitesse du moteur augmente ou diminue à peu près dans les mêmes proportions.
En pratique, on peut réaliser cette variation en alimentant l'induit du moteur M avec une génératrice G de tension variable (Fig. 28-5).
Figure 28-5 Commande de vitesse Ward-Leonard
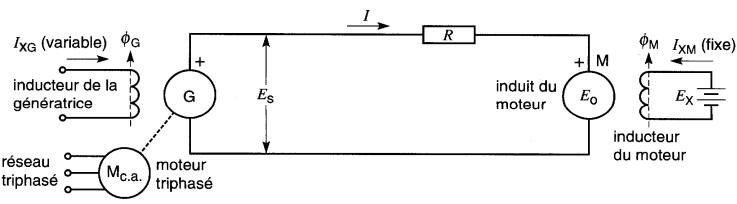
La génératrice est entraînée par un moteur à courant alternatif Mc.a, qui reçoit son énergie du réseau. On maintient l'excitation IXM de l'inducteur du moteur M constante, alors que l'on fait varier celle (IXG) de la génératrice.
On peut même changer le sens de rotation du moteur en inversant la polarité de la tension Es, produite par la génératrice. Cette inversion de polarité est obtenue par simple inversion du courant d'excitation IXG.
L'ensemble des trois machines Mc.a - G - M de la Fig. 28-5 constitue un groupe Ward-Leonard. Cette méthode assure une extrême souplesse dans le réglage de la vitesse entre de très grandes limites.
On l'utilise pour le contrôle des moteurs de laminoirs et d'ascenseurs dans les mines et les grands édifices. La flexibilité du système Ward-Leonard provient du fait qu'il permet de forcer le moteur M à développer à la fois la vitesse et le couple requis par la charge.
Supposons, par exemple, que Es soit ajusté à un niveau légèrement supérieur à Eo. Le courant I circule alors dans le sens indiqué à la Fig. 28-5 et le moteur produit un couple positif. Le moteur absorbe de la puissance car le courant I entre par la borne positive de l'induit.
Supposons maintenant que l'on réduise l'excitation du générateur de sorte que Es devienne inférieur à Eo. Le courant change de sens, ce qui inverse le couple développé par le moteur.
Simultanément, le moteur devient une génératrice, car le courant sort par la borne positive. La puissance électrique que le «moteur» M fournit à G provient de l'énergie cinétique emmagasinée dans le moteur et sa charge. Sous l'effet du couple négatif, le moteur décélère rapidement. (Voir explications section Notions de mécanique et Thermodynamique.)
Comme la «génératrice» G reçoit de la puissance, elle fonctionne en moteur, entraînant le moteur à courant alternatif qui fonctionne à son tour en générateur. Par conséquent, de la puissance à courant alternatif est retournée au réseau. Cette possibilité de récupérer l'énergie est particulièrement efficace, et constitue un autre avantage du groupe Ward-Leonard.
Exemple 28-3
Le système Ward-Leonard montré à la Fig. 28-5 comprend un moteur à courant continu de 2000 kW et un générateur (le 2500 kW. La résistance totale du circuit reliant les deux induits (y compris leur propre résistance) est de 10 mΩ.
Le moteur tourne à une vitesse de 300 r/min lorsque Es est de 500V.
Calculer le couple et la vitesse du moteur M :
a) lorsque Es = 400V et Eo = 380V
b) lorsque Es 350V et Eo = 380V
Solution
a) Le courant dans l'induit est :
I = (Es - Eo) / R = (400 - 380) / 0,01 = 2000 A
La puissance fournie au moteur est:
Pm =EoI= 380 x 2000 = 760 kW
La vitesse approximative du moteur est:
n = 380V/500V x 300 = 228 r/min
d'où le couple du moteur:
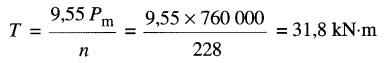
b) Lorsque Es = 350 V, le courant dans l'induit est:
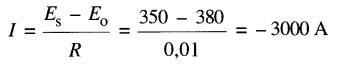
Le courant est négatif, donc il circule dans le sens inverse, produisant ainsi un couple négatif. La vitesse du moteur est encore 228 r/min car Eo = 380V.
Cependant, à cause du couple négatif, le moteur est freiné et sa vitesse commence à décroître. Le moteur renvoie au reste du système une puissance
Pm = EoI = 380 x 3000 = 1140 kW
dont la plus grande partie PG = 3000 x 350 = 1050 kW est fournie à la génératrice.
Le reste est dissipé dans la résistance de 10 mΩ. Comme le couple est proportionnel au courant dans l'induit, le moteur développe un couple de :
T = 3000A / 2000A x 31,8 kN•m = 41,8 kN•m
Une autre façon de faire varier la tension aux bornes de l'induit d'un moteur pour contrôler sa vitesse, consiste à placer un rhéostat en série avec celui-ci (Fig. 28-6).
Figure 28-6 Commande de vitesse par rhéostat en série avec l'induit
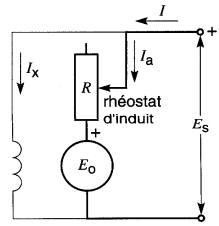
Le passage du courant dans le rhéostat crée une chute de tension qui, soustraite de la tension de la source, réduit la tension aux bornes du moteur. Cette méthode permet seulement de réduire la vitesse à partir de la vitesse nominale.
Elle est onéreuse à cause de la puissance dissipée inutilement par effet Joule dans le rhéostat. De plus, la régulation de vitesse est très mauvaise. En effet, la chute de tension dans le rhéostat augmente à mesure que le courant de l'induit augmente, d'où une baisse substantielle de vitesse avec la charge.
Exemple 28-4
Soit un moteur à c.c. de 2 kW, 240V, 1500 r/min, à excitation shunt. Il doit entraîner une charge à une vitesse de 975 r/min, tout en développant un couple de 5 N •m.
On utilise le montage de la Fig. 28-6, avec Es = 240V.
Calculer la valeur approximative de la résistance R et la puissance qu'elle dissipe.
Solution
Comme le moteur doit tourner à 975 r/min, la tension induite Eo doit être environ:
Eo = 975 / 1500 x 240 V = 156 V
La tension aux bornes de R est donc:
ER = 240 - 156 = 84V
La puissance mécanique développée par le moteur est:
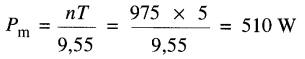
Le courant d'induit est:
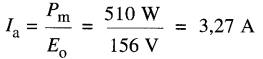
Il s'ensuit que R est donnée par:
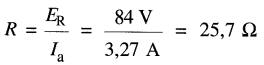
La résistance dissipe une puissance de :
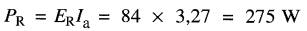
Réglage de la vitesse par le flux de l'inducteur
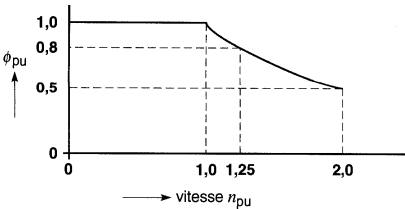
Une autre façon de faire varier la vitesse est de changer le flux θ. En effet, si la tension E, de la source est tenue constante, le numérateur de l'expression reste constant.
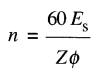 (28-5)
(28-5)
Par conséquent, la vitesse de rotation n du moteur devient inversement proportionnelle au flux θ. Quand le flux augmente, la vitesse diminue et vice versa.
Cette méthode de variation de la vitesse est fréquemment employée car elle est très simple et ne requiert qu'un rhéostat d'excitation peu coûteux. Le rhéostat est branché en série avec l'inducteur (Fig. 28-7).
Figure 28-7 Commande de vitesse par rhéostat en série avec l'inducteur shunt
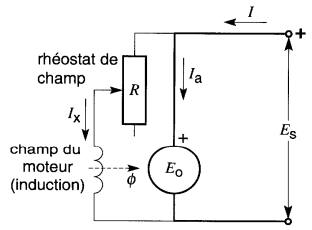
Si l'on augmente la résistance du rhéostat, le courant d'excitation et le flux diminuent.
Cet affaiblissement du flux réduit la tension induite E0, ce qui fait augmenter temporairement le courant Ia dans l'induit. Le moteur développe un couple plus grand qu'auparavant et il accélère jusqu'à ce que la tension E0 redevienne presque égale à la tension E, de la source.
Pour développer la même f.c.é.m. que précédemment avec un flux plus faible, le moteur doit tourner plus vite. Il est donc possible d'élever la vitesse d'un moteur au-dessus de sa vitesse normale en intercalant une résistance dans le circuit de l'inducteur.
Ce mode de réglage permet de faire varier la vitesse de certains moteurs shunt dans un rapport de 3 à 1. Une variation plus grande entraîne des problèmes de stabilité et de commutation. On notera ici que lorsque la valeur du flux θ se rapproche de zéro, le moteur tend à atteindre une vitesse extrêmement élevée, à s'emballer. Cette condition peut entraîner la destruction du moteur.
Si le courant d'excitation est interrompu dans l'inducteur d'un moteur shunt, le flux correspondant à l'aimantation rémanente devient tellement faible que le moteur doit tourner à une vitesse dangereusement élevée pour induire une f.c.é.m. suffisante.
Des dispositifs de protection, montés sur l'arbre du moteur, peuvent prévenir cet emballement en ouvrant le circuit d'alimentation.
Marche du moteur shunt en charge
Lorsqu'une charge mécanique est subitement appliquée à l'arbre d'un moteur shunt tournant à vide, le faible courant à vide ne peut produire un couple suffisant pour entraîner cette charge, et le moteur ralentit.
La force contre-électromotrice diminue alors, ce qui provoque le passage d'un courant plus intense dans l'induit. Le courant augmente jusqu'à ce qu'il produise un couple suffisant pour supporter la charge mécanique à entraîner.
En résumé, plus la charge mécanique appliquée est grande, plus la vitesse diminue, et plus le courant dans l'induit est intense. La vitesse d'un moteur shunt est relativement constante, même pour des charges variables. Dans la plupart des cas, elle diminue seulement de l'ordre de 5 à 15 % lorsque la pleine charge est appliquée.
La Fig. 28-8 montre les caractéristiques typiques d'un moteur shunt.
Figure 28-8 Caractéristiques en charge d'un moteur shunt
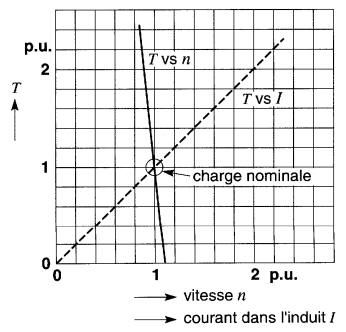
La courbe donnant les valeurs relatives du couple T en fonction de la vitesse n indique que la vitesse varie seulement de 1,1 p.u. à 0,9 p.u. lorsque le couple augmente de zéro à 2 p.u. La deuxième courbe montre que le couple est proportionnel au courant d'induit dans la région comprise entre zéro et 2 p.u.
Cependant, cette droite se transforme progressivement en une courbe aplatie lorsque le courant dépasse 2 p.u.
En effet, la réaction d'induit devient tellement intense que le flux 0 (éq. 28-4) diminue, même si le courant d'excitation demeure fixe. Dans le cas des gros moteurs, la diminution de flux θ due à la réaction d'induit se fait déjà sentir à pleine charge. Par conséquent, la vitesse de ces moteurs tend à augmenter avec la charge.
Comme cela risque de produire une instabilité lorsque la charge varie, on ajoute à ces moteurs un enroulement série qui impose une diminution de vitesse lorsque la charge croît. Ce genre de moteur s'appelle moteur shunt stabilisé. La Fig. 28-9 montre deux moteurs couplés de 4100 kW utilisés pour la propulsion d'un brise-glace.
La Fig. 28-10 illustre l'utilisation de moteurs à c.c. dans un laminoir à chaud.
Figure 28-9 Deux moteurs de 4100 kW couplés propulsent le brise-glace russe «Kiev» (gracieuseté de Siemens)

Figure 28-10 Laminoir à chaud. Le laminage est effectué par 6 laminoirs consécutifs actionnés chacun par un moteur à c.c. de 2500 kW. La feuille d'acier laminé est ensuite entraînée vers la gauche par 161 moteurs à c.c. de 3 kW

Démarrage d'un moteur shunt
On a vu que si la pleine tension est appliquée à un moteur au repos, l'appel de courant est énorme. On risque alors de faire sauter les fusibles, de brûler l'induit et d'endommager le collecteur.
Pour tout moteur shunt à courant continu, il faut donc prendre des précautions appropriées pour limiter le courant de démarrage à une valeur raisonnable, de l'ordre de 1,5 à 2 fois le courant nominal.
Pour réduire le courant au démarrage, il suffit de monter en série avec l'induit un rhéostat de démarrage. La résistance introduite est ensuite progressivement diminuée à mesure que le moteur accélère, et finalement enlevée du circuit dès que le moteur atteint sa vitesse de régime permanent.
Pour assurer un couple de démarrage satisfaisant, il faut que le flux soit aussi grand que possible, c'est-à-dire que l'inducteur doit être connecté directement à la source d'alimentation. Ces conditions sont remplies dans le montage de la Fig. 28-11.
Figure 28-11 Rhéostat de démarrage pour moteur shunt
Aujourd'hui, on utilise plutôt des circuits électroniques pour limiter le courant de démarrage et pour régler la vitesse (chapitre 43).
Démarreur manuel pour moteur shunt
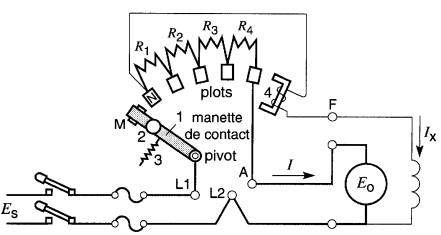
La Fig. 28-11 montre le schéma d'un rhéostat de démarrage ainsi que la manière de le raccorder à un moteur shunt. Ce rhéostat est du type à plots; les plots en cuivre sont reliés aux extrémités des résistances RI , R2, R3 etR4.
Lorsque la manette de contact 1 est sur le plot mort M, le circuit du moteur est ouvert.
Lorsqu'on déplace la manette au moyen de la poignée 2, elle vient d'abord en contact avec le plot N. La pleine tension ES est alors appliquée aux bornes du champ shunt.
En même temps, un courant I commence à circuler dans l'induit. Ce courant est limité par la somme des quatre résistances plus la résistance Ro de l'induit. Le moteur accélère, et le courant I diminue progressivement. On fait alors avancer la manette au plot suivant et le courant prend de nouveau une valeur relativement élevée.
À mesure que la vitesse du moteur augmente, on passe ainsi d'un plot à l'autre, pour amener finalement la manette au dernier plot. Elle y est retenue par l'attraction d'un petit électro-aimant 4, branché en série avec l'inducteur.
Si la tension de la source d'alimentation est soudainement interrompue, ou si l'excitation de la bobine shunt est coupée accidentellement, l'électro-aimant n'est plus alimenté et la manette est rappelée par le ressort 3 sur le plot mort. Ce dispositif est nécessaire pour éviter que le moteur ne reparte intempestivement au retour de la tension.
Moteur série
La construction d'un moteur série est identique à celle d'un moteur shunt, sauf en ce qui concerne l'inducteur. L'inducteur est connecté en série avec l'induit et, par conséquent, il doit porter le plein courant du moteur (Fig. 28-12).
Figure 28-12 a. Schéma de connexions d'un moteur série sans pôles de commutation ; b. Diagramme schématique d'un moteur série, montrant l'induit et le champ série
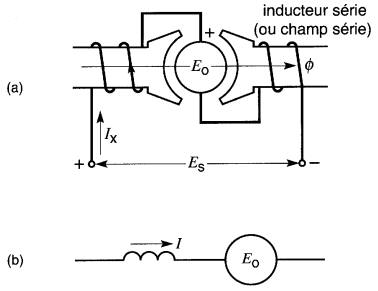
L'enroulement série est donc composé de quelques spires de fil de gros calibre. Bien que sa construction soit similaire à celle d'un moteur shunt, les caractéristiques d'un moteur série sont complètement différentes.
Dans un moteur shunt, le flux 0 par pôle est constant pour toute charge normale, car l'inducteur shunt est connecté à la source de tension, laquelle est fixe. Mais dans un moteur série, le flux dépend du courant qui circule dans l'induit; par conséquent, le flux croît avec le courant de charge.
Malgré ces différences, les même équations fondamentales s'appliquent aux deux machines. Lorsqu'un moteur série fonctionne à pleine charge, le flux par pôle est le même que celui d'un moteur shunt de même puissance et de même vitesse.
Cependant, lors du démarrage, le courant d'induit est supérieur au courant nominal; le flux est donc supérieur au flux obtenu à pleine charge. Par conséquent, le couple de démarrage d'un moteur série excède celui d'un moteur shunt. Par contre, lorsque la charge est inférieure à la puissance nominale, le courant d'induit et le flux par pôle sont inférieurs aux valeurs normales.
Cet affaiblissement du flux a le même effet qu'une réduction de l'excitation dans un moteur shunt et impose une vitesse supérieure à la valeur nominale.
Par exemple, si le courant d'un moteur série diminue de la moitié de sa valeur nominale, le flux 0diminue également de moitié, de sorte que la vitesse double. Il est clair que si la charge mécanique est faible, la vitesse risque d'atteindre des valeurs dangereuses.
Pour cette raison, on ne doit jamais permettre à un moteur série de fonctionner à vide. Il a tendance à s'emballer, et les forces centrifuges peuvent arracher les enroulements de l'induit et provoquer la destruction de la machine.
Lors du démarrage, tout comme pour le moteur shunt, il faut limiter le courant au moyen d'un rhéostat; les connexions sont cependant plus simples à cause de l'absence d'enroulement shunt. Pour le démarrage manuel, on peut employer un rhéostat de démarrage semblable à celui de la Fig. 28-11.
L'électro-aimant 4 qui retient la manette de contact doit être connecté en série avec l'induit. De cette façon, lorsque le courant d'induit devient trop faible (indication de survitesse) la manette retourne automatiquement à la position ouverte.
Réglage de la vitesse d'un moteur série
Lorsque le moteur série entraîne une charge, sa vitesse peut être augmentée en branchant une résistance faible en parallèle avec l'enroulement inducteur. Le courant circulant dans l'enroulement série est alors affaibli ce qui provoque une diminution de flux et une augmentation de vitesse.
De la même façon, la vitesse peut être diminuée en branchant une résistance en série avec l'induit et l'inducteur
La Fig. 28-13 donne les caractéristiques en charge typiques d'un moteur série. Remarquer que la vitesse a augmente en flèche lorsque le couple T diminue. Noter aussi que la caractéristique couple-courant n'est pas linéaire, mais a plutôt une forme parabolique.
Figure 28-13 Caractéristiques en charge d'un moteur série.
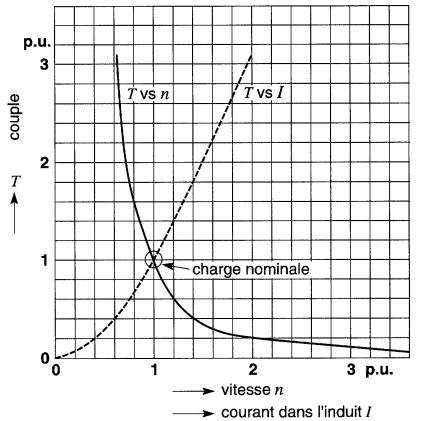
Exemple 28-5
Un moteur série de 15 hp, 240V, 1780 r/min a un courant nominal de 54A.
Ses caractéristiques en charge sont données par les courbes normalisées de la Fig. 28-13.
Calculer:
a) la valeur du outrant et de la vitesse lorsque le couple est de 24 N.m
b) le rendement du moteur dans ces circonstances
Solution
a) Établissons d'abord la puissance de base, la vitesse de base et le courant de base du moteur.
Ces valeurs correspondent aux spécifications nominales du moteur, soit:
PB = 15 hp = 15 x 746 = 11 190 W
nB = 1780 r/min
IB =54A
Le couple de base est donc:
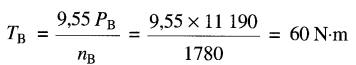
Le couple de 24 N•m correspond à un couple relatif de
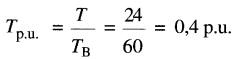
En se référant à la Fig. 28-13, un couple de 0,4 p.u. correspond à une vitesse de 1,4 p.u. La vitesse réelle est donc:
n = np.u. x nB = 1,4 x 1780 = 2492 r/min
On note sur la caractéristique T-I, qu'un couple de 0.4 p.u. requiert un courant de 0,6 p.u.
Le courant est donc:
I = Ip.u. x IB = 0,6 x 54 = 32,4A
b) Pour calculer le rendement, il faut connaître les valeurs de la puissance électrique P1 et de la puissance mécanique P2.
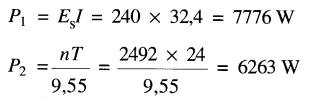
Le rendement est donc:
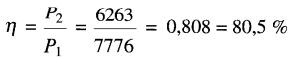
Emploi du moteur série
Le moteur série est utilisé chaque fois qu'une charge exige un couple de démarrage puissant ou une accélération rapide. Il est aussi employé dans les cas où sa propriété d'atteindre une haute vitesse à faible charge est avantageuse. Le moteur série convient particulièrement bien à la traction, comme dans les locomotives électriques et les voitures de métro (Fig. 28-14).
Figure 28-14 Voiture électrique
La voiture est munie de 2 moteurs série de 114 kW, 360 V c.c.
Autres spécifications des moteurs:
vitesse: 0 à 3160 r/min; isolation: classe 155 °C; refroidissement: à l'air ; masse: 650 kg. utilisée sur les trains du métro de Montréal
La mise en marche est rapide car, aux faibles vitesses le couple est élevé. Le moteur série ralentit dans les côtes et, de ce fait, il ne tire pas un courant trop élevé.
En terrain plat, il atteint une vitesse beaucoup plus grande. On l'emploie également pour la commande d'engins de levage tels que grues, palans, cabestans. Lorsqu'il actionne une grue, les charges légères sont déplacées rapidement alors que les charges lourdes sont déplacées lentement.
Moteur compound
Le moteur compound porte un inducteur série et un inducteur shunt. La FMM de l'enroulement série agit toujours dans le même sens que celle de l'enroulement shunt. La FMM de l'enroulement shunt est habituellement plus grande que celle du champ série, même à pleine charge.
La Fig. 28-15 donne le schéma d'un moteur compound.
Figure 28-15 a. Schéma des connexions d'un moteur compound avec pôles de commutation; b. Diagramme schématique d'un moteur compound avec pôles de commutation.
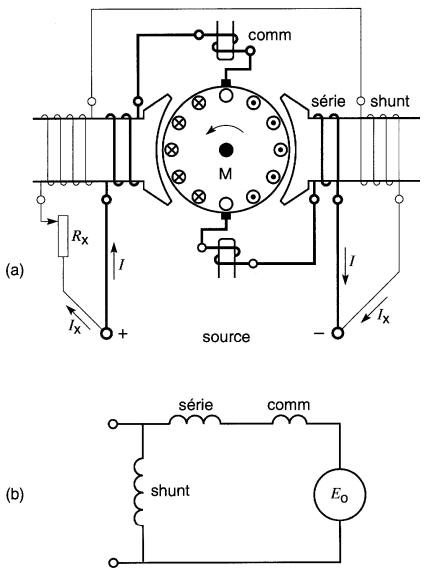
Lorsque le moteur tourne à vide, le courant I dans l'enroulement série est faible et sa FMM est négligeable devant celle de l'inducteur shunt. Dans ces conditions, le moteur agit comme un moteur shunt: il ne s'emballe donc pas à vide.
À mesure que la charge augmente, la FMM de l'inducteur série croît, alors que celle de l'inducteur shunt reste constante. La FMM totale du champ est donc plus grande en charge qu'à vide, de même que le flux. Le moteur doit donc ralentir. La diminution de vitesse de la marche à vide à la pleine charge est généralement de l'ordre de 20 % à 30 %.
Le moteur compound sert à entraîner des machines présentant une charge très élevée et de courte durée: étaux-limeurs, cisailles, poinçonneuses, presses, etc.
Ces machines comportent souvent un volant d'inertie qui emmagasine de l'énergie mécanique et la restitue lorsque de fortes surcharges sont brusquement appliquées; les moteurs compound permettent cet échange d'énergie car leur vitesse tombe au moment de la surcharge.
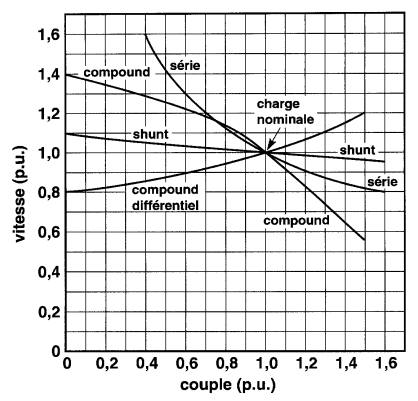
Le graphique de la Fig. 28-16, donnant les courbes caractéristiques des vitesses des moteurs shunt, série et compound, illustre bien l'influence du champ série sur la vitesse.
Figure 28-16 Caractéristiques vitesse-couple de divers types de moteurs à c.c.
Inversion du sens de rotation
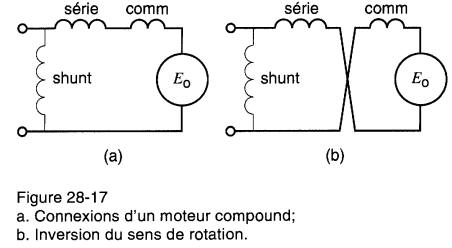
Si l'on désire changer le sens de rotation d'un moteur shunt, il faut inverser le sens du courant, soit dans l'induit, soit dans l'inducteur. Dans le cas d'un moteur compound, il faut inverser le sens du courant dans l'induit (Fig. 28-17). Il est entendu que le terme «induit» comprend les pôles de commutation.
Figure 28-17 a. Connexions d'un moteur compound; b. Inversion du sens de rotation
Énergie cinétique de rotation et arrêt d'un moteur
Lorsqu'un moteur démarre une charge ayant une inertie importante, comme un gros volant, on constate qu'il faut attendre plusieurs minutes avant qu'il n'atteigne sa vitesse de régime permanent.
Si l'on coupe l'alimentation du moteur, la période de décélération est encore plus longue, et peut atteindre une heure et plus. Le temps requis pour amener la charge à la vitesse finale, ou pour l'arrêter, dépend de l'énergie cinétique emmagasinée.
Lors du démarrage, la charge reçoit de l'énergie du moteur mais, à cause de son couple limité, il faut attendre un temps appréciable avant que la vitesse finale soit atteinte.
De même, lors du ralentissement, si les pertes par friction et par ventilation sont faibles, une longue période doit s'écouler avant que cette énergie cinétique soit dissipée. Une décélération lente est bien souvent inacceptable; on doit alors appliquer un couple de freinage pour assurer un arrêt rapide.
On pourrait évidemment freiner le moteur à l'aide d'un frein mécanique. Une autre approche, évitant l'usure mécanique, consiste à freiner le moteur en faisant circuler dans l'induit un courant de sens approprié. Pour effectuer ce freinage électromécanique, on peut utiliser deux méthodes:
a) le freinage dynamique
b) le freinage par inversion («plugging»)
Freinage dynamique
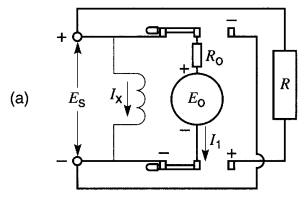
Considérons un moteur shunt à excitation séparée raccordé à une source de tension ES. Le sens du courant I1 dans l'induit et la polarité de la tension induite Eo sont tels qu'indiqués sur la Fig. 28-18a.
Figure 28-18
a. Moteur alimenté par une source ES;
b. Moteur débranché de la source ; il continue à tourner grâce à son inertie ;
c. Induit raccordé à une résistance R.
L'énergie cinétique est dissipée dans la résistance sous forme de chaleur.
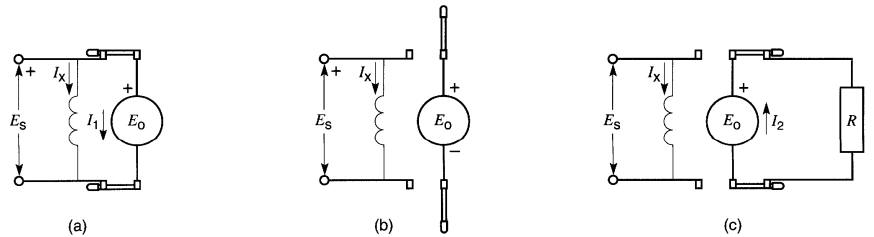
Si l'on néglige la résistance de l'induit, la tension induite est sensiblement égale à la tension ES de la source.
Si l'on coupe l'alimentation de l'induit (Fig. 28-18b), le moteur continue à tourner, sa vitesse diminuant graduellement sous l'effet des pertes par frottement. D'autre part, le champ étant toujours alimenté, la tension induite diminue au même rythme que la vitesse. Le moteur devient alors une génératrice qui fonctionne à vide.
Si maintenant on raccorde l'induit à une résistance extérieure R (Fig. 28-18c), la machine fonctionne toujours en génératrice et la tension induite Eo produit un courant d'induit I2 circulant dans le sens inverse du courant original I1. Il en résulte un couple de freinage d'autant plus grand que le courant I2 est grand.
En pratique, on choisit une résistance R telle que le courant de freinage initial soit environ 2 fois le courant nominal. Dans ces conditions, le couple de freinage initial est le double du couple normal du moteur.
À mesure que le moteur ralentit, la décroissance progressive de la tension Eo produit une diminution correspondante du courant I2. Le couple de freinage devient de plus en plus faible et il atteint finalement une valeur nulle lorsque l'induit cesse de tourner.
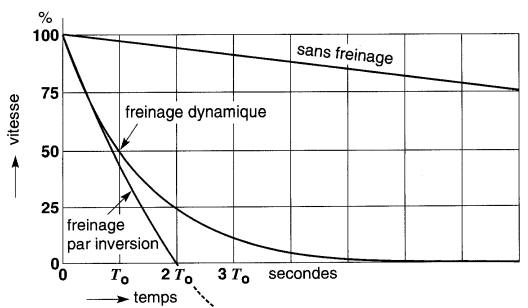
Le freinage dynamique provoque donc une décroissance de la vitesse qui est rapide au début, et lente vers la fin.
Afin d'illustrer l'efficacité de cette méthode de freinage, nous avons représenté sur la Fig. 28-19 les courbes de décélération obtenues par freinage dynamique et en débranchant simplement le moteur de la source. 28.17
Figure 28-19 Taux de décroissance de la vitesse selon le genre de freinage utilisé
Freinage par inversion
On peut arrêter un moteur encore plus rapidement en utilisant le freinage par inversion.
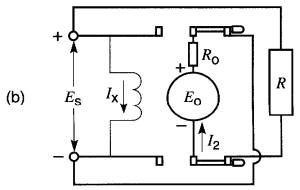
Cette méthode consiste à inverser brutalement le sens du courant dans l'induit en intervertissant les bornes de la source (Fig. 28-20).
Figure 28-20
a. Moteur
alimenté par une source ES.
b. Moteur
alimenté par la source, mais dans le sens inverse.
En marche normale (moteur), le courant I1 absorbé par l'induit vaut:
I1 = (ES - Eo)/Ro, où Ro représente la résistance de l'induit.
Si l'on intervertit subitement les bornes de la source, la tension résultante agissant sur l'induit devient (Eo + ES). Cette tension fera aussitôt circuler dans le sens inverse un courant dont la valeur est
I = (Eo + ES )/Ro.
Si l'on ne prenait aucune mesure pour le limiter, ce courant serait énorme, plus de 50 fois supérieur à l'intensité normale. Il produirait un arc autour du collecteur provoquant la destruction des lames, des balais et de leurs supports avant même que les disjoncteurs de sécurité aient le temps d'ouvrir le circuit.
Pour éviter une telle catastrophe, il faut introduire une résistance R en série avec l'induit au moment où l'on intervertit les bornes (Fig. 28-20b).
Comme pour le freinage dynamique, sa valeur est ajustée de façon à limiter le courant initial de freinage I2 à environ 2 fois le courant nominal.
Avec ce montage, contrairement au freinage dynamique, un couple est développé même à l'arrêt.
En effet, pour une vitesse nulle, Eo = 0 et I2 = ES /R, soit environ la moitié de sa valeur initiale.
Dès que le moteur s'arrête, il faut ouvrir immédiatement l'interrupteur, sinon le moteur repart en sens inverse.
Habituellement, cette ouverture est commandée automatiquement par un dispositif sensible à la vitesse nulle. Les courbes de la Fig. 28-19 permettent de comparer le freinage par inversion avec le freinage dynamique, le courant initial étant le même dans les deux cas.
On constate que le freinage par inversion arrête le moteur complètement à un instant où la vitesse par freinage dynamique vaut encore 25 % de sa valeur originale. Cependant, la grande simplicité du freinage dynamique le rend plus populaire dans la plupart des applications.
Constante de temps mécanique d'un système de freinage
Lorsqu'on utilise le freinage dynamique, la vitesse d'un moteur décroît exponentiellement avec le temps. On peut alors définir un demi-temps mécanique To similaire au demi-temps électrique d'un circuit RC.
La valeur de To est le temps requis pour que la vitesse du moteur tombe à 50 % de sa valeur précédente. Connaissant la valeur de To, il est facile de tracer la courbe de décroissance de la vitesse en suivant la méthode expliquée à la section 19-7 de la section Inductance.
On peut prouver que la valeur de To est donnée par:
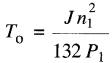 (28-6)
(28-6)
où
To = temps requis pour que la vitesse du moteur tombe à la moitié de sa valeur initiale [s]
J = moment d'inertie du moteur et de sa charge, rapporté à l'arbre du moteur [kg.m²]
n1 = vitesse au début du freinage [r/min]
P1 = puissance de freinage initiale développée par l'induit [W]
132 = constante tenant compte des unités [valeur exacte = (30/π)² /loge²]
Cette équation suppose que le freinage est attribuable entièrement à la puissance dissipée dans la résistance.
En pratique, les pertes par frottement et aération s'ajoutent à cette puissance de sorte que le temps d'arrêt est plus court que celui indiqué par l'équation 28-6.
Noter que la puissance de freinage est en tout temps égale au produit de la tension Eo générée dans l'induit et du courant initial circulant dans celui-ci.
Exemple 28-6
Un moteur à c.c. de kW. 250 V, 1200 r/min entraîne une charge possédant une grande inertie dont la valeur totale, rapportée à l'arbre du moteur est de 177 kg•m².
En régime normal, le moteur est branché à une source de 210V, et sa vitesse est de 1280 r/min. On utilise une résistance extérieure de 0,2Ω pour arrêter le moteur par freinage dynamique.
Calculer:
a) la valeur du temps To
b) le temps requis pour que la vitesse tombe à 80 r/min
c) Estimer le temps requis pour atteindre 80 r/min sans freinage dynamique, sachant que les pertes par frottement, par aération et dans le fer sont de 8 kW
Solution
a) Avant le moment du freinage, la tension aux bornes de l'induit est de 210V, et la vitesse est de 1280 r/min. Lorsque l'induit est subitement branché sur la résistance de 0,2Ω, la tension induite Eo est encore près de 210V.
Le courant initial lors du freinage est:
I= Eo / R = 210V / 0,2Ω = 1050A
La puissance de freinage initiale de l'induit est donc :
P = EoI = 210 x 1050 = 220,5 kW
Le demi-temps To est donné par l'équation 28-6 :
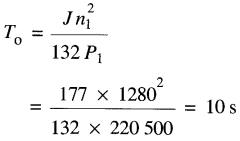
b) Il s'ensuit que la vitesse du moteur diminue de moitié pour chaque intervalle de 10 s.
Le tableau suivant donne la vitesse et le temps correspondant.
vitesse [r/min] temps [s]
1280
0
640
10
320
20
160
30
80
40
On constate que la vitesse atteint 80 r/min après une période de 40 s.
c) Les pertes par frottement, par aération et dans le fer ne varient pas exactement de la même façon que les pertes joules dans une résistance de freinage.
Cependant, leur comportement est semblable, ce qui nous permet de faire une estimation du temps de freinage.
On a:
n1 = 1280 r/min P1 = 8000 W
Le nouveau temps T1/2 est:
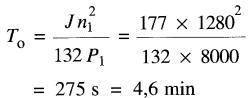
Le temps d'arrêt augmente en proportion de To. Par conséquent, le temps requis pour atteindre 80 r/min est:
t = 275 s / 40 s x 40s = 1100 s
Théoriquement, il faut un temps infini pour freiner un moteur dont la vitesse décroît de façon exponentielle ; en pratique, on peut considérer que la machine s'arrête après un intervalle égal à 5To.
Si le moteur est freiné par inversion, on peut prouver que le temps d'arrêt est donné par :
ts = 2To (28-7)
où
ts
= temps de freinage par inversion [s]
To
= «demi-temps» mécanique du système [s]
Exemple 28-7
Dans l'exemple 28-6, on se propose d'utiliser le freinage par inversion. On choisit une résistance de freinage de 0,4Ω alun que le courant de freinage initial reste le même qu'auparavant.
Calculer:
a) la puissance de freinage initiale P1
b) le temps requis pour arrêter le moteur
Solution
a) La tension aux bornes de la résistance au début du freinage est:
E = Eo + Es = 210 + 210 = 420V
Le courant initial de freinage est:
i = E / R = 420 / 0,4 = 1050A
La puissance initiale de freinage développée par l'induit est:
P1 = EoI = 210 x 1050 = 220,5 kW
D'après l'équation 28-6, il s'ensuit que la valeur de To demeure inchangée, donc To = 10 s.
b) Le temps pour arrêter la machine complètement est alors:
T = 2To = 2 x 10 = 20s
Dans certains systèmes de commande, il faut que le moteur puisse changer de vitesse avec une extrême rapidité. Dans ces circonstances, on a intérêt à réduire l'inertie de l'induit au minimum (Fig. 28-21).
Figure 28-21 Induit de moteur à c.c. ultra-rapide. Son inertie a été réduite au minimum en supprimant le noyau d'acier traditionnel. Ne comportant plus que les enroulements et le collecteur, l'induit peut accélérer de zéro à 1200 r/min en 1 milliseconde

Enroulement de compensation
Certains moteurs de 100 kW à 10 000 kW, utilisés pour entraîner les laminoirs, sont soumis a des cycles de fonctionnement très exigeants. Ils doivent accélérer, décélérer, s'arrêter, changer de sens de rotation dans des temps très courts.
Donc, le courant circulant dans l'induit augmente, diminue et change de sens de façon saccadée, ce qui provoque de brusques variations de la réaction d'induit. Pour ces moteurs, les pôles de commutation ne suffisent pas à maîtriser complètement la réaction d'induit.
On doit faire appel à un enroulement de compensation raccordé également en série avec l'induit mais logé dans la face des pièces polaires (Fig. 28-22).
Figure 28-22 Moteur à 6 pôles avec enroulements de compensation logés dans des encoches taillées dans la face des pôles. La machine possède en outre 6 pôles de commutation. Ces deux enroulements compensent, point par point, la FMM créée par induit

Tout comme l'enroulement de commutation, cet enroulement produit une FMM égale et opposée à la FMM de l'induit. Cependant, puisqu'il est réparti dans plusieurs encoches, la FMM de l'induit est annulée point par point, ce qui permet d'éviter la distribution inégale du champ observée à la Fig. 27-19.
L'ajout d'un enroulement de compensation a une grande influence sur la conception et la performance d'un moteur à c.c. :
1. La longueur de l'entrefer peut être réduite car on n'a plus à se soucier de l'effet de la réaction d'induit sur le champ de l'inducteur;
2. L'inductance du circuit de l'induit est réduite par un facteur 4 ou 5; par conséquent, le courant dans l'induit peut changer plus rapidement, ce qui assure une meilleure réponse de la machine ;
3. Le couple crête peut atteindre 3 ou 4 fois le couple nominal du moteur. Le couple crête d'un moteur non compensé est limité à des valeurs nettement plus faibles en raison de la réaction d'induit qui affaiblit le flux ¢ provenant de l'inducteur;
4. Lors des changements de couple brusques, la possibilité de créer un arc entre les balais à la surface du collecteur est réduite.
L'enroulement de compensation est donc essentiel sur les gros moteurs à c.c. qui doivent subir des variations de charges très brusques.
Moteurs à aimant permanent
Nous avons vu que dans un moteur shunt le champ magnétique est produit par un courant d'excitation circulant dans les bobines excitatrices. L'énergie dépensée, la chaleur dégagée et l'espace relativement important occupé par ces bobines constituent parfois des inconvénients du moteur à c.c. conventionnel.
On peut éviter ces inconvénients en remplaçant les bobines par des aimants permanents. Il en résulte un moteur plus petit et qui ne risque pas de s'emballer à cause d'une défaillance du champ. De plus, comme la perméabilité des aimants est presque égale à celle de l'air, la longueur effective de l'entrefer est augmentée des dizaines de fois.
Par conséquent, la réaction d'induit crée un champ magnétique beaucoup plus faible que celui résultant de l'utilisation de pièces polaires en fer doux. Le champ créé par les aimants ne subit donc pas la forte distorsion montrée à la Fig. 27-19.
Par conséquent, la commutation et la capacité de surcharge du moteur sont améliorées. Un dernier avantage provient du fait que l'inductance de l'induit est réduite, ce qui diminue le temps de réponse de la machine lors des changements rapides du courant d'induit.
Mentionnons toutefois deux inconvénients de ce type de moteur: le coût relativement élevé des aimants et l'impossibilité d'augmenter la vitesse du moteur en réduisant le champ magnétique.
Les moteurs à aimant permanent sont particulièrement utiles dans la gamme des puissances inférieures à 5 kW. Les aimants utilisés sont en céramique (ferrite) ou en alliage de terres rares et de cobalt. La Fig. 28-23 montre la construction d'un moteur de 1,5 hp, 90 V, 2900 r/min. Son induit allongé assure une faible inertie et une réponse rapide dans les systèmes asservis.
Figure 28-23 Moteur à aimant permanent de 1,5 hp, 90 V, 2900 r/min, 14,5 A.
Nombre d'aimants: 2; type d'aimant: ferrite; diamètre de l'induit : 73 mm; longueur de l'induit: 115 mm; nombre d'encoches: 20; nombre de lames du collecteur : 40; nombre de spires par bobine : 5; conducteur: n° 17 AWG; type d'enroulement : imbriqué; résistance de l'induit à 20 °C = 0,34Ω

PRINCIPES FONDAMENTAUX DES ENTRAÎNEMENTS ÉLECTRIQUES
Les quatre quadrants de fonctionnement
Nous venons de voir les divers équipements utilisés pour le démarrage et l'arrêt des moteurs à courant continu. Nous avons vu aussi qu'il existe des applications industrielles où un moteur doit fonctionner à des vitesses et couples variables, parfois dans les deux sens de rotation.
En plus d'agir comme moteur, la machine doit fonctionner comme générateur ou comme frein pendant de courts intervalles. Par exemple, dans une locomotive électrique le moteur peut tourner dans le sens horaire ou antihoraire et le couple peut agir soit dans le même sens que la rotation, soit dans le sens opposé.
En d'autres mots, la vitesse et le couple peuvent être positifs ou négatifs, indépendamment l'un de l'autre. C'est au moyen d'un graphique que l'on peut le mieux décrire le comportement d'un entraînement électrique.
Les vitesses positives et négatives sont affichées sur l'axe horizontal, tandis que les couples positifs et négatifs sont représentés sur l'axe vertical. Les deux axes séparent le graphique en quatre quadrants de fonctionnement, identifiés respectivement quadrants 1, 2.3 et 4 (Fig. 28-24).
Figure 28-24 Un système d'entraînement électrique peut fonctionner dans les 4 quadrants
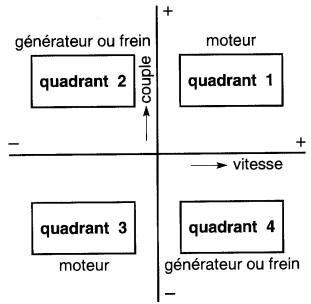
Lorsqu'une machine fonctionne dans le quadrant 1, le couple et la vitesse sont positifs, de sorte que ces deux grandeurs agissent dans le même sens (disons dans le sens horaire). Par conséquent, une machine fonctionnant dans ce quadrant fonctionne nécessairement en moteur: elle fournit de la puissance mécanique à la charge.
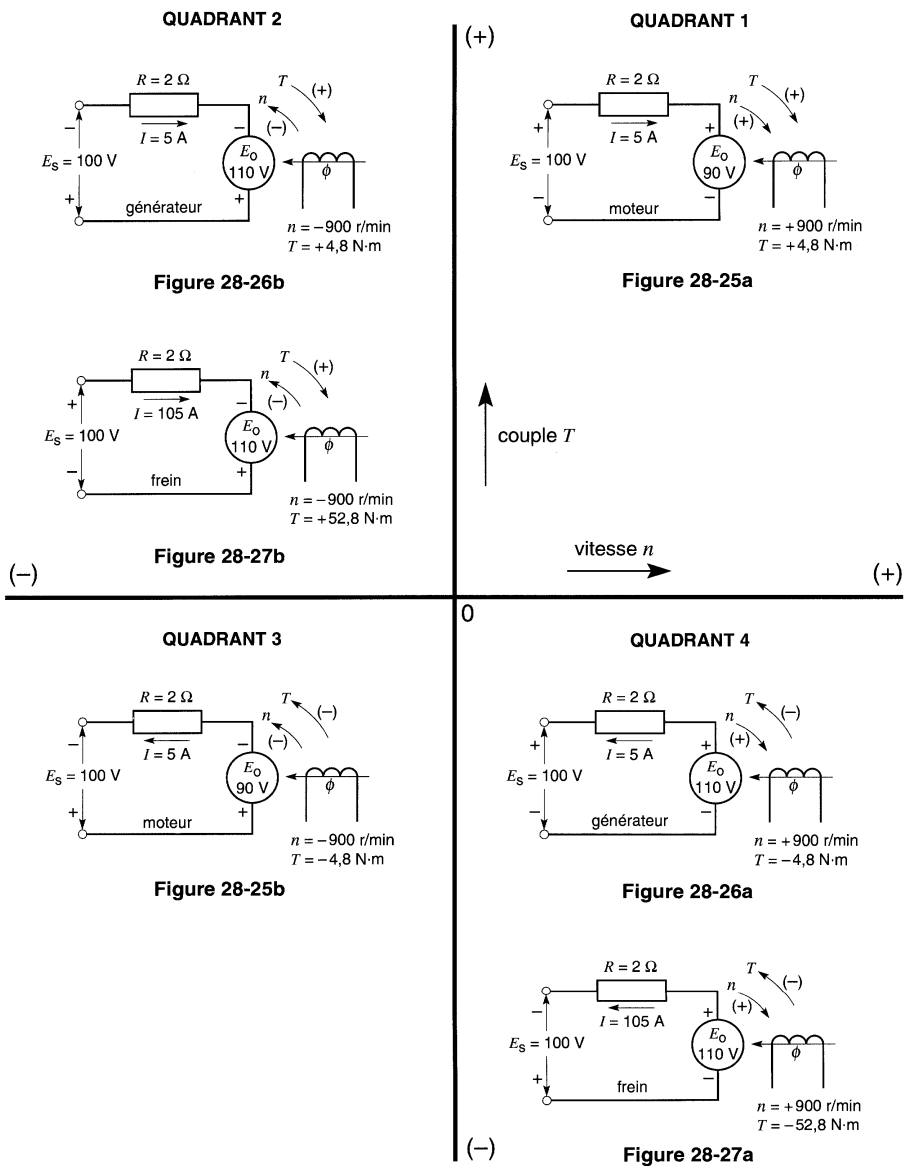
La Fig. 28-25a montre le circuit de la machine lorsqu'elle fonctionne comme moteur.
La tension Es de la source est légèrement supérieure à la tension induite Eo, de sorte que le courant I entre par la borne positive (+). La résistance de l'induit étant R, la valeur du courant I est donnée par:
I = (Es - Eo)IR
Une machine fonctionne aussi en moteur dans le quadrant 3, sauf que le couple et la vitesse sont tous deux inversés par rapport au quadrant 1 (Fig. 28-25b).
Dans le cas illustré, on a simplement changé la polarité de la source Es. Lorsque le moteur fonctionne dans le quadrant 4, sa vitesse est positive alors que le couple est négatif (Fig. 28-26a).
Le moteur fonctionne donc comme générateur. Cette condition se produit lorsque la tension induite Eo est plus grande que celle de la source. Par conséquent, le courant sort par la borne (+) de Eo.
Puisque le courant entre par la borne (+) de la source, la puissance débitée par la machine est fournie à la source, sauf pour la faible portion dissipée dans la résistance R.
Dans ces circonstances, le moteur ralentit, et on dit qu'il y a freinage par récupération d'énergie. À mesure que la machine ralentit, l'énergie cinétique des parties tournantes est retournée au réseau d'alimentation. Dans le cas des gros moteurs, on préfère ce mode de freinage à celui où l'énergie est simplement dissipée en chaleur.
Toujours dans le quadrant 4, si l'on intervertit la polarité de Es, la polarité de Eo agit dans le même sens que celle de la source (Fig. 28-27a).
La valeur du courant est maintenant I = (Es + Eo)IR
Il en résulte un gros courant qui circule dans le sens indiqué. Le moteur débite une puissance E0I en même temps que la source débite une puissance ESI. La somme de ces deux puissances est dissipée dans la résistance R.
Dans ces circonstances, même si le moteur fonctionne encore en générateur, on dit qu'il agit en frein parce que la puissance électrique qu'il génère est entièrement convertie en chaleur dans la machine.
Le rendement est nul et l'induit du moteur surchauffe rapidement. Lorsque le moteur fonctionne dans le quadrant 2, les conditions sont analogues à celle du quadrant 4, sauf que la polarité des tensions, le sens des courants, la vitesse et le couple sont inversés. Les valeurs données dans les Fig. 28-25, 28-26 et 28-27 servent uniquement à illustrer les principes de fonctionnement.
Courbe du couple en fonction de la vitesse
La courbe du couple en fonction de la vitesse d'un moteur shunt à c.c. illustre bien les différents modes de fonctionnement de la machine comme moteur, comme génératrice ou comme frein.
En se référant à la courbe (1) de la Fig. 28-28, la machine agit comme moteur dans le quadrant 1, comme frein dans le quadrant 2 et comme génératrice dans le quadrant 4.
En intervertissant la polarité de la source (ou en intervertissant les bornes de l'induit ou du champ), on obtient la courbe (2) montrée en pointillé. La machine fonctionne alors comme moteur dans le quadrant 3, comme génératrice dans le quadrant 2 et comme frein dans le quadrant 4.
Cela démontre que. selon les connexions, la machine peut fonctionner comme frein ou comme génératrice dans les quadrants 2et4. Les systèmes d'entraînement à vitesse variable sont conçus pour faire varier graduellement la vitesse et le couple, afin de satisfaire aux exigences de la charge.
On atteint cet objectif en déplaçant la courbe (1) horizontalement, vers la gauche ou vers la droite, selon le besoin. Dans le cas d'une machine shunt, ce déplacement est obtenu en faisant varier la tension de la source qui alimente l'induit, en gardant le champ fixe.
Lorsque la tension augmente, la vitesse augmente, et la courbe (1) se déplace vers la droite, tout en gardant la même pente. En effet, la pente demeure la même tant que la résistance de l'induit et le flux de l'inducteur shunt demeurent constants. Cela décrit précisément le comportement du moteur M dans le système Ward Leonard discuté plus loin.
Courbes T - n relatives en p.u.
Le couple T et la vitesse n sont les deux principales caractéristiques d'un moteur.
Comme il existe une grande variété de machines, dont la puissance, la tension, la vitesse et le champ magnétique peuvent varier dans une gamme importante, il est utile de relativiser ces différentes grandeurs. Il s'agit alors d'exprimer ces grandeurs en unités relatives (p.u.).
Pour développer la courbe T-n en p.u., choisissons un moteur shunt à excitation séparée (Fig. 28-29).
Figure 28-29 Schéma d'un moteur shunt montrant les grandeurs relatives de tension, courant, flux, vitesse et couple
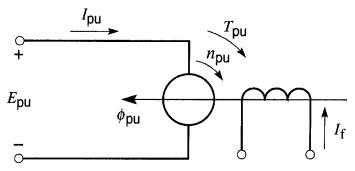
Il se prête bien à une commande de la vitesse et du couple. Toutefois, on doit respecter les limites de performance de la machine. Ainsi, on ne doit pas dépasser les va- leurs nominales du courant d'induit, de la tension d'induit, ni du flux de l'inducteur.
On peut évidement utiliser des valeurs inférieures. La tension E aux bornes de l'induit, le courant I dans l'induit, le flux 0 et la vitesse n sont exprimés en valeurs relatives (p.u.).
Par exemple, si la tension nominale E est de 240 V et le courant nominal I de 600 A, ces deux grandeurs auront une valeur relative de 1. De même, si le flux 0a une valeur nominale de 5 mWb, sa valeur relative est aussi de 1 . Dans les explications qui suivent, nous utiliserons les symboles suivants pour la notation des valeurs réelles et relatives :
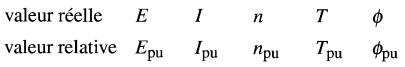
L'avantage du système p .u. est qu'il permet de formuler des relations simples entre ces différentes grandeurs, et d'en déduire une courbe couple-vitesse universelle. On sait, par exemple, que le couple T est proportionnel m produit du flux Φ et du courant d'induit I.
En valeurs relatives, on peut donc écrire:
Tpu = Φpu X Ipu (28-8)
sait aussi que la tension E de l'induit est proportionnelle au produit de la vitesse n et du flux Φ.
En valeurs relatives, on peut donc écrire :
Epu = npu X Φpu (28-9)
point de départ logique sur la courbe relative T-n (Fig.28-30) correspond à celui où le moteur développe son couple nominal
(Tpu = 1) à la vitesse nominale (npu = 1).
La vitesse nominale constitue la vitesse de base («base speed»).
Pour faire décroître la vitesse en dessous de sa valeur nominale, on diminue graduellement la tension Epu de 1 à zéro, tout en gardant constants le courant d'induit et le flux (Ipu = 1, Φpu= 1 ).
En appliquant la formule 28-8, on trouve que le couple relatif Tpu est alors égal à 1 :
Tpu =0pu X Ipu = 1 x 1 = 1
Cela indique que durant cette phase d'opération (Fig . 28-30), le couple conserve sa valeur nominale.
Donc, lorsque la vitesse npu est comprise entre zéro et 1, le moteur fonctionne dans le mode dit à couple constant. Durant la même phase d'opération, et d'après la for- mule 28-9, la tension relative Epu est donnée par:
Epu = npu X Φpu = npu x 1 = npu
Comme Epu = npu, on obtient une droite inclinée à 45°.
Les Fig. 28-30 et 28-31 montrent les relations entre Epu, npu, Ipu et Φpu, pendant le mode à couple constant (pour npu plus petit que 1,0).
Figure 28-30 Tension et courant relatifs en fonction de la vitesse relative
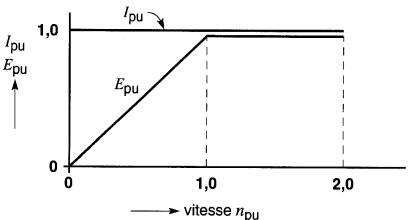
Figure 28-31 Flux relatif en fonction de la vitesse relative