Chapitre 2 - loi d'ohm

Chapitre 2 - loi d'ohm

Ce chapitre explique comment la valeur d'un courant I circulant dans un circuit dépend de la résistance R du circuit et de la tension V appliquée à ses bornes.

Il traite en particulier de la loi I = V/R découverte en 1828 d'après les expériences de Georg Simon Ohm; si l'on connaît deux quelconques des trois facteurs V, I, R, on peut calculer le troisième.

La loi d'Ohm permet également de calculer la puissance électrique dissipée dans un circuit.

Dans les sections suivantes, on fournira des détails supplémentaires.

2.1 Le courant I = V / R

2.2 La tension V = IR

2.3 La résistance R = V / I

2.4 Unités pratiques

2.5 Unités multiples et sous-multiples

2.6 Loi de proportionnalité entre V et I

2.7 La puissance

2.8 Dissipation de puissance dans une résistance

2.9 Secousse électrique

2.1 LE COURANT I = V / R

Supposons un circuit dont la résistance reste inchangée, mais dont la tension varie: le courant variera également. Le circuit présenté à la figure 2-1 est une démonstration de cette affirmation.

Figure 2-1 Lorsque la tension V augmente, le courant I augmente, ce qui conduit l'ampoule à éclairer plus brillamment.

La tension V appliquée peut, par exemple, varier de 0 à 12 V. La lampe a un filament de 12V qui utilise normalement la tension maximale pour que le courant produit donne un éclairage normal.

L'appareil de mesure I indique la valeur du courant dans le circuit alimentant la lampe.

Lorsqu'une tension de 12V est appliquée, la lampe éclaire ce qui correspond à un courant normal. Lorsque la tension V est réduite à 10V, la lampe éclaire moins puisque le courant I est plus faible.

Plus la tension V décroît, plus l'éclairage fourni par la lampe diminue. Lorsqu'une tension nulle est appliquée, aucun courant ne circule et l'ampoule ne peut pas éclairer.

En résumé, la modification de brillance de l'ampoule montre que le courant varie lorsque la tension appliquée change.

D'une manière générale, quels que soient V et R, la loi d'Ohm est l'expression suivante:

I = V / R

dans laquelle I est la valeur du courant traversant la résistance R branchée aux bornes de la source de différence de potentiel V.

Les unités pratiquement utilisées pour V et R étant le volt et l'ohm, la valeur du courant I sera alors exprimée en ampères.

Ainsi:

Ampères = volts / ohms

Cette formule s'énonce comme suit:

pour obtenir la valeur en ampères du courant traversant R, il suffit de diviser la tension (différence de potentiel) en volts appliquée aux bornes de R par la résistance en ohms de R.

À la figure 2-2, par exemple, une tension de 6V est appliquée aux bornes d'une résistance R de 3Ω.

La valeur en ampères du courant I traversant cette résistance sera, par application de la loi d'Ohm, de 6/3 = 2A.

Figure 2-2 En utilisant la loi d'Ohm:

(a) source de tension appliquée aux bornes de la résistance R;

(b) schéma comportant les valeurs calculées à partir de la loi d'Ohm.

Tension élevée, mais courant faible

II est important de remarquer que pour des tensions élevées le courant obtenu peut être faible lorsque la résistance du circuit est très importante.

Par exemple, l'application d'une tension de 1000V aux bornes d'une résistance de 1 000 000Ω fera conduire un courant de seulement 1/ 1000 A.

L'application de la loi d'Ohm donne en effet:

Tension faible, mais courant fort

Inversement, une tension très faible appliquée aux bornes d'une résistance très faible peut conduire à des courants très importants.

Une batterie de 6V branchée aux bornes d'une résistance de 0,01Ω produit un courant de 600A:

I = V / R = 6V / 0,01Ω = 600A

L'intensité I décroît lorsque R croît

Remarquons également les valeurs de I dans les deux exemples donnés ci-après:

Exemple 1

Un radiateur ayant une résistance de 8Ω est branché aux bornes du secteur à 120V.

Quelle est la valeur du courant I?

Réponse

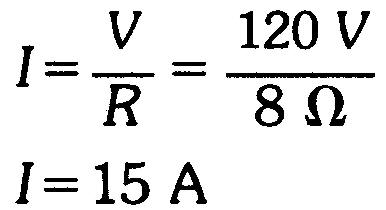
Exemple 2

Une petite ampoule ayant une résistance de 2400Ω est branchée aux bornes de cette même source de tension à 120V.

Quelle est la valeur du courant I?

Réponse

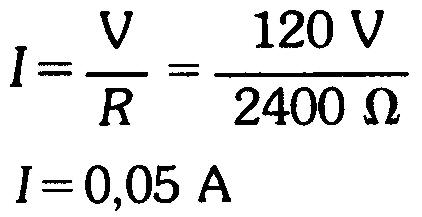
Dans ces deux exemples, la tension appliquée aux bornes est la même, mais on peut noter que le courant, dans l'exemple 2, est beaucoup plus faible par suite de la valeur plus élevée de la résistance.

Problèmes pratiques 2.1 (réponses à la fin du chapitre)

Pour ces problèmes, V est la tension appliquée aux bornes d'une résistance R traversée par le courant I:

(a) V= 100V, R = 25Ω. Calculer I;

(b) V= 50V, R = 25Ω. Calculer I;

(d) V= 100V, R = 5Ω. Calculer I.

2.2 LA TENSION V = IR

En se reportant à la figure 2-2, on voit que la valeur de la tension aux bornes de R doit être égale à V puisque la résistance est branchée directement aux bornes de la batterie.

La valeur numérique de cette tension V est égale I x R.

L'Annexe D, Mathématiques, explique comment effectuer la transformation des équations.

Par exemple, à la figure 2-3, la tension IR est égale à 2A x 3Ω = 6V, soit la tension V appliquée.

Figure 2-3 La résistance d'une portion quelconque du circuit est égale à son rapport V/I.

La formule est la suivante:

V = IR (2.2)

Le courant I étant exprimé en ampères et la résistance R en ohms, le produit V est en volts. Il doit bien en être ainsi car la valeur I, égale à V/R, permet au produit IR d'égaler la tension aux bornes de R.

Outre les calculs numériques que la formule IR permet d'effectuer, il est commode de considérer que ce produit IR correspond à une tension.

Chaque fois qu'un courant circule dans une résistance, il doit exister, entre les deux bornes de cette résistance, une différence de potentiel de valeur égale au produit IR.

S'il n'y avait pas de différence de potentiel aux bornes de la résistance, aucun électron ne pourrait circuler: il n'y aurait donc pas de courant.

Problèmes pratiques 2.2 (réponses à la fin du chapitre)

Pour ces problèmes, V est ta tension appliquée aux bornes d'une résistance R traversée par le courant I:

(a) I = 0,002A, R = 1000Ω. Calculer V;

(b) I = 0,004A, R = 1000Ω. Calculer V;

2.3 LA RÉSISTANCE R = V / I

II existe une troisième et dernière version de la loi d'Ohm dans laquelle les trois facteurs V, I, R sont reliés par la formule:

R = V / I

À la figure 2-2, R est égal à 3Ω puisque la tension de 6V appliquée aux bornes de la résistance produit la circulation d'un courant de 2 A dans celle-ci.

Lorsque V et I sont connus, on peut calculer la résistance qui est égale à la tension aux bornes de R divisée par le courant la traversant.

Physiquement, une résistance peut être considérée comme une certaine substance dont les éléments ont une structure atomique qui, soumise à une force plus ou moins grande, permet la circulation d'électrons libres à travers cette résistance.

Électriquement, toutefois, il est plus commode de considérer simplement la résistance comme le rapport V / I.

Un élément quelconque qui autorise la circulation d'un courant de 1A pour une tension appliquée de 10V a une résistance de 10Ω.

Ce rapport V / I de 10Ω est la caractéristique de cet élément.

Si la tension est doublée, donc portée à 20V, la valeur du courant doublera également et atteindra 2A; le rapport V / I conduira à la même résistance de 10Ω.

De plus, pour étudier les effets d'une résistance dans un circuit, il n'est nullement besoin de connaître sa structure physique; il suffit de connaître son rapport V /I .

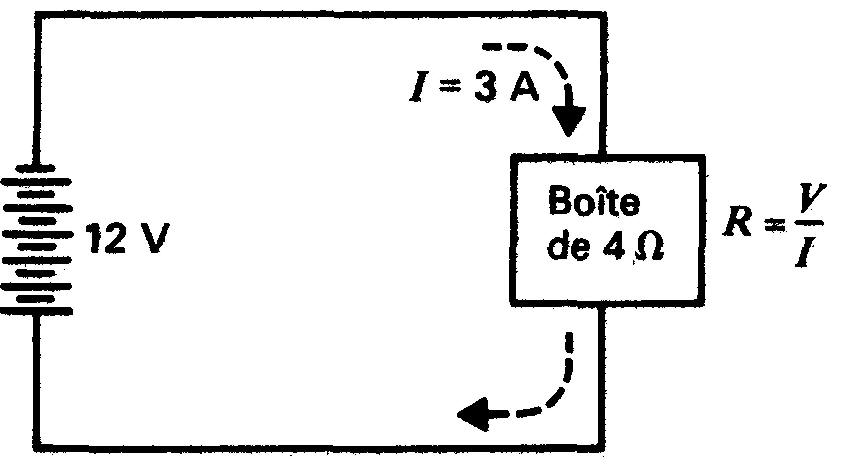
Cette notion est illustrée à la figure 2-3.

La figure représente une boîte contenant une certaine substance inconnue, branchée dans un circuit qui permet de mesurer la tension de 12 V appliquée aux bornes de la boîte et le courant de 3 A qui la traverse.

La résistance est égale à 12 V /3 A, soit 4Ω.

La boîte peut contenir un liquide, un gaz, un métal, de la poudre ou tout autre matériau; électriquement, c'est une résistance de 4Ω car son rapport V / I est de 4.

Problèmes pratiques 2.3 (réponses à la fin du chapitre)

Pour ces problèmes, V est la tension appliquée aux bornes d'une résistas ce R traversée par le courant I;

(a) V = 12 V, I = 0,003 A. Calculer R;

(b) V = 12 V, I =0,006 A. Calculer R;

2.4 UNITÉS PRATIQUES

Les trois formes de la loi d'Ohm permettent de définir les unités pratiques de courant, de différence de potentiel et de résistance de la manière suivante:

un ampère = un volt / un ohm

un volt = un ampère x un ohm

un ohm = un volt / un ampère

Un ampère est la valeur du courant traversant une résistance de un ohm soumise, entre ces bornes, à une différence de potentiel de un volt.

Un volt est la valeur de la différence de potentiel appliquée à une résistance de un ohm parcourue par un courant de un ampère.

Un ohm est la valeur qu'offre une résistance, de rapport V / I égal à 1, au passage d'un courant de un ampère lorsqu'elle est soumise à une différence de potentiel de un volt.

En résumé, le diagramme circulaire de la figure 2-4 illustrant la relation V = IR facilite l'usage de la loi d'Ohm.

Remarquer que V occupe toujours la position supérieure pour V = IR, V/R = I ou V/I = R

Figure 2-4 Cercle mnémotechnique de V = IR, V/I = R, ou V/R = I.

Problèmes pratiques 2.4 (réponses à la fin du chapitre)

Pour ces problèmes V est la tension appliquée aux bornes d'une résistance R parcourue par le courant I:

(a) V = 0,007 A, 7? = 5000 ù. Calculer V;

(b) V= 12 000 V, R = 6 000 000 Ω. Calculer I;

2.5 UNITÉS MULTIPLES ET SOUS-MULTIPLES

Les unités de base (ampère, volt et ohm) sont les unités pratiquement utilisées dans l'étude des circuits de puissance; dans de nombreuses applications électroniques, ces unités sont toutefois trop grandes ou trop petites.

Par exemple, les résistances peuvent atteindre plusieurs millions d'ohms, la sortie d'une alimentation haute tension d'un téléviseur est d'environ 20 000 V et le courant circulant dans les tubes et transistors est généralement de l'ordre du millième ou du millionième d'ampère.

Dans de tels cas, il est commode d'utiliser des multiples ou des sous-multiples des unités de base.

Le tableau 2-1 montre comment ces unités sont basées sur le système décimal.

Les transformations usuelles relatives à V, I, R sont indiquées sur ce tableau.

On trouvera à l'Annexe E une liste complète de tous les préfixes.

Notons que la lettre majuscule M est utilisée pour représenter 10⁶ et la distinguer de la minuscule «m» utilisée pour représenter 10^-3.

Exemple 3

Un courant I de 8 mA circule à travers une résistance R de 5 Ω, quelle est la valeur de la tension IR?

Réponse V = IR = 8 x 10^-3 x 5 x 10³ = 8 x 5 =

V = 40V

En général, des milliampères multipliés par des kilohms conduisent à un résultat en volts car les facteurs 10^-3 et 10³ s'annulent.

Exemple 4

Quelle est la valeur du courant produit par une tension de 60 V branchée aux bornes d'une résistance de 12 Ω?

Réponse

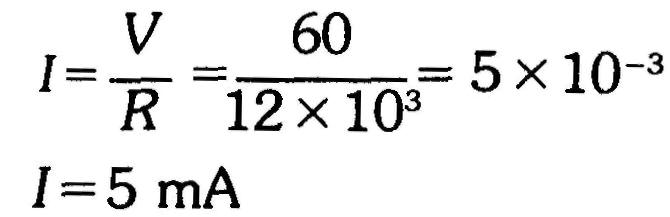
Remarquons que des volts branchés aux bornes de kilohms produisent des milliampères.

De même, des volts branchés aux bornes de mégohms produisent des microampères.

Ces combinaisons communes peuvent être résumées de la manière suivante:

volts / kilohms = milliampères

volts / mégohms = microampères

kilohms x milliampères = volts

mégohms x microampères = volts

Problèmes pratiques 2.5 (réponses à la fin du chapitre)

(a) Convertir les valeurs suivantes en fonction des unités de base et des puissances de 10: 6 mA, 5 kΩ et 3 µA.

(b) Convertir les valeurs suivantes en fonction des unités à préfixe métrique: 6 x 10^-3 A, 5 x 10³ Ω et 3 x 10^-6 A.

2.6 LOI DE PROPORTIONNALITÉ ENTRE V et I

La formule de la loi d'Ohm, I = V/R, établit que V et I sont liés par une loi de proportionnalité directe, quel que soit R.

On peut étudier cette relation entre V et I en utilisant pour R_L une résistance fixe de 2 Ω, comme indiqué à la figure 2-5.

Figure 2-5 Expérience destinée à montrer que I croît en raison directe de V:

(a) circuit comportant une tension V variable et une résistance R constante;

(b) tableau donnant les valeurs croissantes de I pour les valeurs de V croissantes;

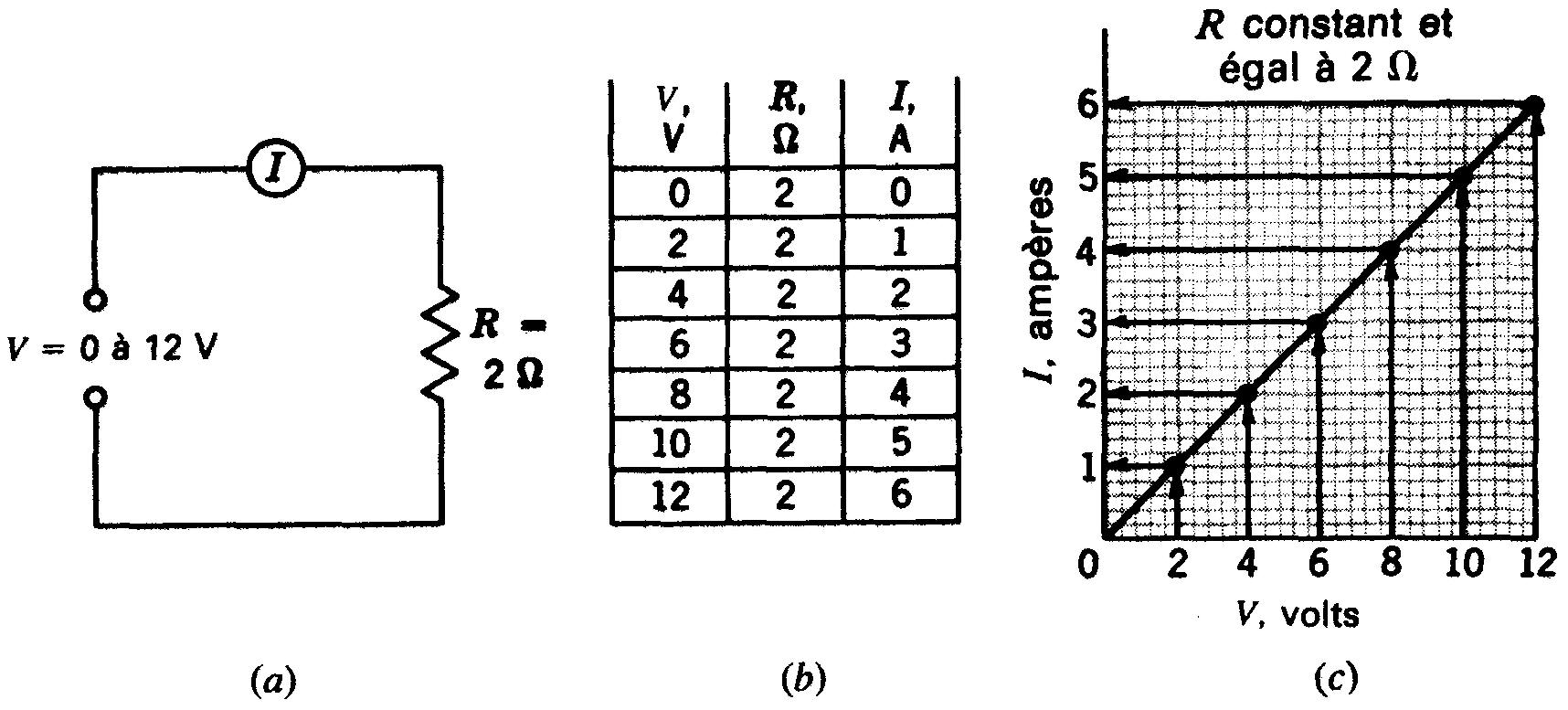
Lorsque l'on fait varier V, l'appareil de mesure indique que le courant I varie proportionnellement à V.

Par exemple, lorsque V vaut 12 V, I est égal à 6 A; lorsque V= 10 V, I = 5 A; lorsque V = 8 V, I = 4 A.

Toutes les valeurs de V et de I obtenues sont indiquées sur le tableau de la figure 2-5b et reportées sur la courbe de la figure 2-5c. Toutes les valeurs de I sont la moitié de la valeur de V puisque R vaut 2 Ω.

Cependant, I = 0 A lorsque V=0 V.

Tracé de la courbe

Les valeurs de la tension V sont reportées sur l'axe horizontal ou axe des x ou abscisse. Les valeurs du courant I sont reportées sur l'axe vertical ou axe des y ou ordonnée.

Comme les valeurs de V et de I sont dépendantes l'une de l'autre, ce sont des facteurs variables. La variable indépendante est V car on assigne des valeurs à la tension et on note le courant obtenu.

Généralement, on porte la variable indépendante sur l'axe des x. C'est pourquoi les valeurs de V sont portées sur l'axe horizontal, alors que les valeurs de I sont portées sur l'axe vertical.

Il n'est pas nécessaire que les deux échelles soient les mêmes. La seule règle à respecter est que, pour chacune des échelles, des longueurs égales représentent des variations d'amplitude égales.

Sur la figure 2-5c, des échelons de 2 V sont utilisés sur l'axe des x, l'axe des y comportant des graduations de 1 A.

Le point 0, à l'origine, est la référence.

Les points de la courbe permettent de retrouver les valeurs du tableau.

Par exemple, le point le plus bas est situé horizontalement à 2 V de l'origine et une intensité de 1 A lui correspond sur l'axe vertical.

De même, le point suivant est situé à l'intersection des droites d'abscisse 4 V et d'ordonnée 2 A.

Une ligne joignant ces deux points comprend toutes les valeurs de I, quelle que soit la valeur de V pour une résistance R de 2Ω.

Ceci s'applique également aux valeurs non contenues dans le tableau.

Par exemple, si l'on prend pour V une valeur de 7 V, l'intersection de la droite d'abscisse 7 V donnera un point de la courbe dont l'ordonnée correspond à un courant I de 3,5 A.

Caractéristique volts-ampères

La courbe montrée sur la figure 2-5c est la caractéristique volts-ampères de R. Elle indique, pour diverses tensions, la valeur de courant admis par la résistance.

On peut cependant utiliser pour V et I des unités multiples et sous-multiples. Dans le cas des transistors et des tubes, on utilise souvent pour I le milliampère ou le microampère.

Résistance linéaire

La caractéristique volts-ampères rectiligne de la figure 2-5 montre que R est une résistance linéaire.

Par définition, une résistance linéaire possède une valeur en ohms constante. Cette valeur n'est pas fonction de la tension appliquée à la résistance.

Dans ce cas, V et I sont directement proportionnels. Doubler la valeur de V de 4 à 8 V fait doubler celle de I de 2 à 4 A.

De la même façon, tripler ou quadrupler la valeur de V fait tripler ou quadrupler la valeur de I. On dispose donc d'un moyen permettant d'augmenter I proportionnellement à V.

Résistance non linéaire Une résistance de ce type présente une caractéristique volts-ampères non linéaire.

La résistance du filament de tungstène d'une ampoule électrique, par exemple, est non linéaire. Cela est dû au fait que R augmente lorsque I augmente, car le filament s'échauffe.

Une augmentation de la tension V appliquée entraîne une augmentation du courant I, mais I n'augmente pas dans la même proportion que V.

Relation inverse entre I et R

Que R soit linéaire ou non, le courant I diminue lorsque R augmente, pour une tension appliquée constante. L'expression relation inverse signifie que I diminue à mesure que R augmente.

Rappelons-nous que dans la formule I = V/R, la résistance figurant au dénominateur.

Lorsque le dénominateur d'une fraction augmente (R, dans le cas présent), la valeur de la fraction (I, dans le cas présent) diminue si son numérateur (V, dans le cas présent) reste constant, ce que nous avons supposé.

Soit, à titre d'exemple, V une tension constante égale à 1 V.

Alors I est égal à la fraction 1/R.

Si R augmente, alors I diminue.

Pour R = 2Ω, I=1/2 A = 0,5 A.

Pour R plus grand, soit R = 10 Ω, I=1/10 A = 0,1 A est donc bien plus petit.

Problèmes pratiques 2.6 (réponses à la fin du chapitre)

Se reporter à la courbe de la figure 2-5c:

(a) Sur quel axe sont portées les valeurs de I?

(b) La résistance R est linéaire ou non linéaire?

2.7 LA PUISSANCE

L'unité de puissance électrique est le watt (W), du nom du physicien James Watt (1736-1819).

Une puissance de un watt correspond au travail effectué pendant une seconde par une différence de potentiel de un volt déplaçant une charge de un coulomb.

Un coulomb par seconde correspondant à un ampère, la puissance en watts est égale au produit des ampères par les volts.
Puissance en watts = volts x ampères

P = V x I (2.4)

Par exemple, une batterie de 6 V produisant un courant de 2 A dans un circuit, fournit une puissance de 12 W.

Étudions les exemples supplémentaires suivants:

Exemple 5

Un grille-pain branché sur le secteur à 120 V consomme 10 A.

Quelle est la puissance consommée?

Réponse

P = V x I= 120 V x 10 A

P=1200W

Exemple 6

Quelle est l'intensité du courant circulant dans le filament d'une ampoule de 300 W branchée aux bornes de secteur à 120 V?

Réponse

P = V x I OU I= P/V, soit:

I = 300 W / 120 V

I=2, 5 A

Exemple 7

Quelle est l'intensité du courant circulant dans une ampoule de 60 W branchée sur le secteur à 120 V?

Réponse P = V x I ou I = P/V, soit:

I = 60W / 120 V

I = 0,5 A

Notons que l'ampoule de plus faible puissance consomme le moins de courant.

Travail et puissance

Le travail et l'énergie sont essentiellement des grandeurs de même nature et utilisent des unités identiques.

La puissance, cependant, est différente car elle correspond à la vitesse d'exécution d'un travail.

Par exemple, si l'on déplace une masse de 100 kg sur une distance de 10 m, le travail effectué est égal à

100 x 9,807 x 10 = 9807 joules quelle que soit la vitesse d'exécution du travail.

Remarquons que l'unité de travail est le joule sans que le temps soit nullement impliqué.

La puissance, toutefois, est égale au travail divisé par le temps nécessaire à son exécution.

Dans l'exemple précédent, si le temps nécessaire à l'exécution du travail est de 1 s, la puissance sera de 9807 W; si la durée du travail est de 2 s, la puissance sera de 4903,5 W.

De la même manière, la puissance électrique est la vitesse à laquelle une tension fait déplacer une charge.

C'est pourquoi la puissance en watts est le produit des volts par des ampères.

La tension spécifie la quantité de travail par unité de charge; la valeur du courant correspond à la vitesse à laquelle se produit le déplacement de la charge.

Unités pratiques de puissance et de travail

Partant du watt, il est aisé d'obtenir d'autres unités importantes.

Le principe fondamental dont il faut se souvenir est que la puissance est reliée au temps mis pour effectuer un travail, alors que le travail est la puissance utilisée pendant un certain temps.

Les formules sont les suivantes:

Puissance = travail / temps (2.5) et Travail = puissance x temps (2.6)

Lorsque l'on utilise le watt comme unité de puissance, le travail correspondant à un watt pendant une seconde est égal à un joule.

Or, un watt correspond à un joule par seconde.

Ainsi, 1 W = 1 J/s.

Le joule est l'unité pratique de base pour le travail et l'énergie.

Dans le cas des électrons isolés, on peut utiliser comme unité de travail Y électron-volt (eV). Remarquer que l'électron est une charge tandis que le volt est une différence de potentiel.

Cette unité correspond à la quantité de travail nécessaire pour déplacer un électron entre deux points dont la différence de potentiel est de un volt.

Comme 6,25 x 10¹⁸ électrons égalent 1 C, et que 1 J égale 1 V x C, 6,25 x 10¹⁸ eV correspondent à 1 J.

Remarquons que l'unité de travail (joule ou électron-volt) est le produit de la charge par la tension, mais que le watt, unité de puissance, est le produit de la tension par le courant.

La division par le temps permettant de transformer le travail en puissance correspond à la division par le temps permettant de transformer la charge en courant.

Kilowatts-heures

C'est une unité habituellement utilisée pour les valeurs importantes de puissance ou d'énergie.

Pour obtenir un résultat en kilowatts-heures, il suffit de multiplier la puissance en kilowatts par le temps d'utilisation de la puissance en heures.

Par exemple, si une ampoule électrique utilise 300 W, soit 0,3 kW, pendant 4 heures (h), la quantité d'énergie est égale à

0,3 x 4, soit 1,2 kWh.

La note d'électricité est établie selon la consommation en kWh. La tension du secteur est constante et égale à 120 V.

Cependant, l'augmentation du nombre de petits appareils et de lampes électriques entraîne une augmentation de la consommation de courant et donc de la puissance, car ils sont tous branchés au secteur.

Supposons que le courant de charge total tiré du secteur soit de 20 A.

La puissance consommée est donc de 20 A x 120 V = 2400 W, soit 2,4 kW.

Si ce courant de charge circule durant 5 h, l'énergie fournie sera de 2,4 x 5 = 12 kWh.

À raison de 0,03 $ le kWh, la note sera de 12 x 0,03 = 0,36 $ pour un courant de charge de 20 A circulant durant 5 h.

Problèmes pratiques 2.7 (réponses à la fin du chapitre)

(a) Un radiateur électrique tire 15 A du secteur à 120 V.

Calculer sa puissance.

(b) Déterminer le courant de charge d'une ampoule de 100 W connectée au secteur à 120 V.

2.8 DISSIPATION DE PUISSANCE DANS UNE RÉSISTANCE

Lorsqu'un courant circule dans une résistance, il se produit un dégagement de chaleur, provoque par le frottement des électrons libres sur les atomes, qui gêne le passage des électrons.

La production de chaleur est une preuve que la production du courant nécessite de la puissance. Ainsi, un fusible se coupe lorsque la chaleur dégagée par un courant trop important fait fondre le fil métallique du fusible.

La puissance est fournie par la source de tension et dissipée dans la résistance sous forme de chaleur. La source de tension doit fournir une puissance égale à la puissance dissipée dans la résistance sous forme de chaleur; dans le cas contraire, la différence de potentiel nécessaire à la production du courant ne pourra être maintenue.

La correspondance entre la puissance électrique et la chaleur est la suivante:

la consommation de 1 W pendant 1 s est équivalente à celle d'une énergie thermique de 1 J.

L'énergie électrique transformée en chaleur est considérée comme dissipée ou consommée parce que l'énergie thermique ne peut être réintroduite dans le circuit sous forme d'énergie électrique.

Puisque la puissance est dissipée dans la résistance d'un circuit, il est commode d'exprimer la puissance en fonction de la résistance.

La formule V x I peut être transformée de la manière suivante:

en remplaçant V par IR, on obtient:

P = V x I = IR x I

P = I²R (2.7)

En remplaçant I par V/R, on obtient:

P = V x I = V x V/R

P = V² / R (2.8)

Dans toutes ces formules, V est la tension aux bornes de R (exprimée en ohms), produisant un courant I exprimé en ampères; la puissance est en watts.

La puissance dissipée dans une résistance peut être calculée en utilisant l'une quelconque des trois formules précédentes; le choix dépendra principalement des facteurs connus au départ.

Sur la figure 2-6, par exemple, la puissance dans la résistance, lorsque le courant qui la traverse est de 2 A pour une tension aux bornes de 6 V, est de 2 x 6 = 12 W.

Figure 2-6 Calcul de la puissance électrique dans un circuit par les formules V x I, I²R ou V²/R.

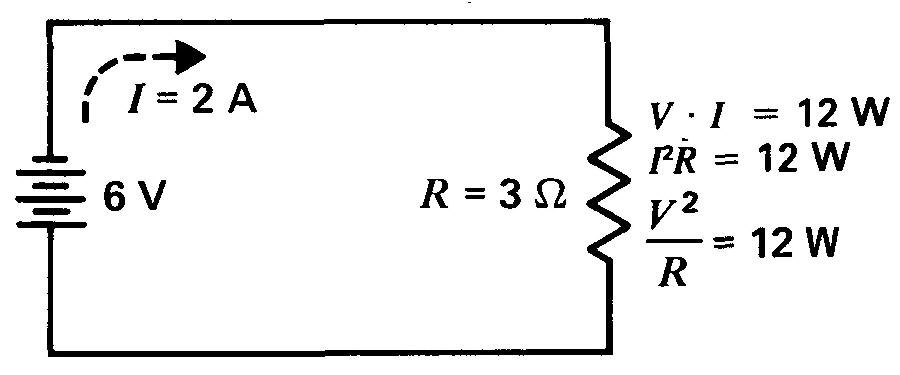
Si l'on effectue le calcul en utilisant seulement le courant et la résistance, la puissance est le produit de 2 au carré, soit 4, par 3, ce qui donne 12 W.

Si l'on emploie seulement la tension et la résistance, on peut calculer la puissance qui sera alors égale à 6 au carré, soit 36, divisé par 3, ce qui donne aussi 12 W.

Peu importe la formule utilisée; une puissance de 12 W est dissipée sous forme de chaleur. Cette puissance doit être fournie en permanence par la batterie pour maintenir une différence de potentiel de 6 V produisant un courant de 2 A malgré l'opposition de 3 Ω.

Dans certaines applications, la dissipation de la puissance électrique est souhaitable car l'appareil doit produire de la chaleur pour remplir son rôle.

Par exemple, un grille-pain de 600 W doit dissiper cette puissance pour fournir la quantité de chaleur nécessaire.

De même, une ampoule d'éclairage de 300 W doit dissiper cette puissance pour chauffer à blanc le filament, permettant ainsi à celui-ci d'être incandescent et de fournir de la lumière.

Dans le cas d'autres applications, cependant, la chaleur peut n'être qu'un sous-produit indésirable obtenu parce que le courant devait traverser une résistance dans un circuit.

Dans tous les cas, chaque fois qu'un courant circule dans une résistance, celle-ci dissipe une puissance égale à PR.

Exemple 8

Calculez la puissance dans un circuit où une source de tension de 100 V produit un courant de 2 A circulant dans une résistance de 50 Ω.

Réponse

P = I²R = 4 x 50

P = 200W

Ceci signifie que la source fournit une puissance de 200 W alors que la résistance dissipe 200 W sous forme de chaleur.

Exemple 9

Calculez la puissance dans un circuit où la même source de tension de 100 V produit un courant de 4 A dans une résistance de 25 Ω.

Réponse

P = I²R = 16 x 25

P = 400W

Remarquons la puissance plus élevée mise en jeu dans l'exemple 9; bien que la résistance R soit inférieure à celle de l'exemple 8, la circulation d'un courant plus important explique le phénomène.

Les dispositifs utilisant la puissance dissipée dans leur résistance, tels que: ampoules d'éclairage, grille-pain, etc., sont habituellement évalués en termes de puissance.

La puissance nominale est exprimée à la tension nominale appliquée, ordinairement celle du secteur, soit 120 V.

Par exemple, un grille-pain de 600 W, 120 V, est calibré de cette manière parce qu'il dissipe une puissance de 600 W dans la résistance de son élément de chauffage lorsqu'il est branché aux bornes d'une tension de 120 V.

Quand il s'agit de calculer I ou R pour des éléments calibrés en puissance pour une tension donnée, il peut être commode d'utiliser les formules de la puissance sous leurs formes transposées.

Il existe trois formules de base pour la puissance, mais les neuf combinaisons suivantes peuvent être obtenues:

Exemple 10

Quel est le courant nécessaire à un, grille-pain de 600 W, 120 V?

Réponse

I = P / V = 600 / 120 = 5A

Exemple 11

Calculez la résistance d'un grille-pain de 600 W, 120V.

Réponse

R = V² / P = 14 400 / 600 = 24 Ω

Exemple 12

Quelle est l'intensité du courant nécessaire pour une résistance de 24 Ω qui dissipe 600 W?

Réponse

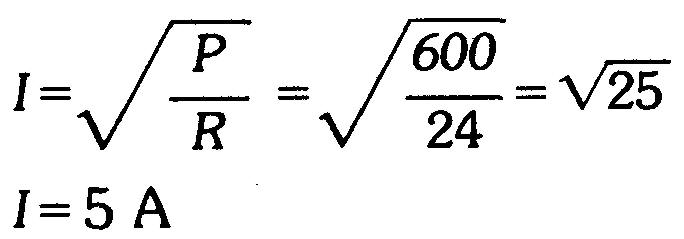
Remarquons que toutes ces formules ne sont que différentes formes de la loi d'Ohm V = IR et celle de la puissance P = VI.

L'exemple suivant qui traite du cas d'une ampoule de 300 W illustre cette notion.

Branché aux bornes du secteur à 120 V, le filament de 300 W absorbe un courant de 2,5 A, soit P/V ou 300/120.

La preuve en est que le produit VI est alors égal à 120 x 2,5 soit 300 W.

Ainsi, la résistance du filament est alors égale à V/I, 120/2,5, soit 48 Ω.

Si on utilise la formule R = V²/P, soit 14 400 / 300, la réponse obtenue est la même: 48 Ω.

Dans tous les cas, lorsque l'ampoule est branchée aux bornes du secteur à 120 V pour qu'elle puisse dissiper sa puissance, elle tire 2,5 A de l'alimentation, et la résistance de son filament chauffé à blanc est de 48 Ω.

Problèmes pratiques 2.8 (réponses à la fin du chapitre)

(a) Soit un courant I de 2 A traversant une résistance R de 5 Ω. Calculer la puissance P dissipée.

(b) Soit une tension V de 10 V appliquée aux bornes d'une résistance R de 5 Ω. Calculer la puissance P dissipée.

2.9 SECOUSSE ÉLECTRIQUE

Lorsque l'on travaille sur des circuits électriques, il existe toujours un risque de recevoir une secousse électrique en touchant les conducteurs sous tension.

La secousse électrique correspond à une contraction soudaine et involontaire des muscles, accompagnée d'une sensation de douleur, provoquée par le passage du courant dans le corps.

Une secousse électrique très importante peut être mortelle.

Le risque de secousse électrique le plus grand provient des circuits à haute tension qui peuvent fournir des puissances considérables.

La résistance du corps humain constitue également un facteur important.

Si l'on tient un conducteur dans chaque main, la résistance du corps aux bornes des conducteurs est d'environ 10 000 à 50 000 Ω.

Si l'on tient les conducteurs plus serrés, la résistance est diminuée.

Si l'on ne tient qu'un seul conducteur, la résistance du corps est beaucoup plus élevée.

Il en découle que plus la résistance du corps est importante, plus le courant qui le traverse est faible.

Ainsi, une règle de sécurité consiste à ne travailler qu'avec une seule main lorsque la tension est appliquée.

De même, lorsqu'on travaille sur un circuit électrique, il faut toujours être isolé de la terre car l'une des extrémités de la ligne est toujours reliée à la terre.

De plus, les châssis métalliques des récepteurs de radio et de télévision sont habituellement reliés à la terre de l'installation électrique. La dernière règle de sécurité — et la meilleure — consiste, dans la mesure du possible, à ne travailler que sur des circuits hors tension et à procéder à des essais de résistance.

Remarquons que la secousse électrique est provoquée par le passage du courant dans le corps et non dans le circuit.

C'est pourquoi les circuits à haute tension sont particulièrement dangereux, car une différence de potentiel suffisante peut produire une intensité de courant importante qui circulera à travers la résistance relativement forte du corps.

Par exemple, une tension de 500 V aux bornes de la résistance de 25 000 Ω du corps produit un courant de 0,02 A, soit 20 mA, qui peut être mortel.

Un courant aussi petit que 10 mA traversant le corps peut donner une secousse électrique.

Une expérience effectuée sur les secousses électriques pour déterminer la valeur du courant à laquelle une personne peut relâcher le conducteur sous tension a montré que les valeurs de ce courant étaient environ de 9 mA pour les hommes et de 6 mA pour les femmes.

De plus, pour les hautes tensions, la puissance pouvant être fournie par la source est un facteur important à considérer sur le plan du danger présenté par une secousse électrique.

Un courant de 0,02 A circulant à travers 25 000 Ω signifie que la résistance du corps dissipe 10 W.

Si la source de tension ne peut fournir 10 W, sa tension de sortie chute lorsque le courant est trop important. L'intensité du courant est alors réduite à la valeur que la source de tension peut fournir.

En résumé, le danger le plus important provient d'une source de tension d'une tension supérieure à 30 V, dont la puissance est suffisante pour maintenir le courant circulant dans le corps lorsque celui-ci est branché aux bornes de la source.

En général, les appareils qui fournissent une puissance importante sont de grande dimension afin de pouvoir dissiper la chaleur.

Problèmes pratiques 2.9 (réponses à la fin du chapitre) Répondre par vrai ou faux:

(a) Pour les secousses électriques, une tension de 120 V est plus dangereuse qu'une autre de 12 V;

(b) Les essais de résistance à l'aide d'un ohm-mètre doivent, si possible, être effectués avec l'alimentation coupée.

Résumé

1. Les trois formes de la loi d'Ohm sont les suivantes: I = V/R, V=RI et R = V/I

Les unités de base sont: le volt pour V, l'ampère pour I, et l'ohm pour R.

2. L'ampère est l'intensité d'un courant produit par une différence de potentiel de un volt appliquée aux bornes d'une résistance de un ohm. Ce courant de 1 A correspond à 1 C/s.

3. La résistance R étant constante, l'intensité du courant I croît en proportion directe de l'augmentation de V. Cette relation linéaire entre V et I est représentée sur la figure 2-5.

4. La tension V étant constante, l'intensité de courant I diminue lorsque la résistance R augmente. Cette relation est appelée la relation inverse entre I et R.

5. La puissance est fonction de la vitesse mise pour effectuer un travail ou utiliser une énergie. Son unité de base est le watt.

Un watt vaut 1 V x 1 A. On a aussi: watts = joules par seconde.

6. L'unité de travail ou d'énergie est le joule. Un joule vaut 1W x 1s

7. Les multiples et sous-multiples les plus utilisés des unités pratiques sont indiqués au tableau 2-1.

8. La tension appliquée aux bornes du corps humain peut provoquer une secousse électrique dangereuse.

Si possible, couper la tension et effectuer des essais de résistance.

Si l'on doit travailler sous tension, n'utiliser qu'une seule main. Ne pas poser la main sur l'autre conducteur.

9. Le tableau 2-2 résume les unités pratiques dans la loi d'Ohm.

Exercices de contrôle

(Réponses aux exercices de contrôle)

Voici un moyen de contrôler si vous avez bien assimilé le contenu de ce chapitre.

Ces exercices sont uniquement destinés à vous évaluer vous-même.

Remplissez les espaces qui se trouvent à la fin des énoncés.

1. Une tension de 10 V est appliquée aux bornes d'une résistance R de 5 Ω; le courant I vaut ______ A.

2. Lorsque 10 V produisent 2,5 A, R est égal à ______ Ω.

3. Lorsqu'un courant de 8 A circule dans une résistance de 2 Ω, la tension IR est égale à ______ V.

4. Une résistance de 500 000 Ω est équivalente à______ MΩ.

5. Une tension de 10 V aux bornes d'une résistance de 5000 Ω produit un courant I de ______mA.

6. Une puissance de 50 W = 2 A x ______V.

7. Une énergie de 50 J = 2 C x ______V.

8. Le courant prélevé sur le secteur à 120 V par un grille-pain de 1900 W= ______ A

9. Un courant de 400 µA = ______ mA.

10. Une tension de 12 V branchée aux bornes d'une résistance R de 2 Ω produit une dissipation de puissance de ______ W.

11. Un courant I de 4 A circule dans, un circuit. Si on double V, R conservant la même valeur, I = ______A.

12. Un courant I de 4 A circule dans un circuit. Si l'on double R, V conservant la même valeur, I =______A.

13. Un récepteur de télévision utilisant 240 W obtenus à partir du secteur à 120 V consomme un courant I de ______ A.

14. Le courant nominal d'une ampoule à 500 W, 120 V, est de______ A.

15. La résistance de cette ampoule est de ______ Ω

16. Une énergie de 12,5 x 1018 eV =______ J.

17. Un courant de 1200 mA =______ A.

18. Dans un circuit amplificateur à tube à vide, la résistance RL de charge de la plaque, d'une valeur de 50 kΩ, a une tension de 150 V à ses bornes. Le courant circulant à travers RL est alors de ______ mA.

19. Dans un circuit à transistor, une résistance R1 de 1 kΩ est traversée par un courant de 200 µA.

La tension aux bornes de R1 = ______V.

20. Dans un circuit à transistor, la tension aux bornes d'une résistance R2 de 50 kΩ est de 6 V. Le courant circulant à travers R2 =______mA.

Questions

1. Donner les trois formes de la loi d'Ohm reliant V, I et R.

2. (a) Pour quelle raison un courant plus important circule-t-il dans une résistance aux bornes de laquelle une tension plus forte est appliquée?

(b) Pourquoi, pour une même tension appliquée, une augmentation de résistance provoque-t-elle une diminution de courant?

3. Calculer la résistance d'une ampoule de 300 W branchée aux bornes du secteur à 120 V en utilisant deux méthodes différentes pour obtenir le résultat.

4. Donner, pour chacun des couples suivante, l'unité la plus grande:

(a) volt ou kilovolt; (b) ampère ou milliampère; (c) ohm ou mégohm; (d) volt ou microvolt; (e) Siemens ou microsiemens; f) électron-volt ou joule; (g) watt ou kilowatt; (h) kilowatt-heure ou joule; (i) volt ou millivolt; (j) mégohm ou kilohm.

5. Indiquer deux mesures de sécurité à observer lorsque l'on travaille sur des circuits électriques.

6. Quelle est la différence entre le travail et la puissance? Indiquer deux unités pour chacun de ces termes.

7. Reportez-vous aux deux résistances montées en série sur la figure 3-1. Quelle est la valeur du courant traversant R2 si le courant circulant dans R1 vaut 2 A?

8. Démontrer que 1 kWh est égal à 3,6 x 106 J.

9. Un circuit comporte une résistance R de 5000 Cl, V variant de 0 à 50 V par échelons de 10 V.

Faire un tableau donnant les valeurs de I pour chaque valeur de V.

Tracer ensuite une courbe en portant les valeurs recueillies en milliampères et les volts.

(La courbe obtenue doit être semblable à la courbe de la figure 2-5c.)

Problèmes
(Réponses aux problèmes de numéro impair)

1. Une source de 90 V est branchée aux bornes d'une résistance de 30 kΩ.

(a) Dessiner le schéma,

(b) Quelle est l'intensité du courant circulant dans la résistance?

(d) Quelle sera l'intensité du courant circulant dans le circuit si l'on triple la résistance?

2. Une batterie de 6 V est branchée aux bornes d'une résistance de 2Ω.

(a) Dessiner le schéma,

(b) Calculer la puissance dissipée dans la résistance,

(d) Quelle sera la valeur de la puissance si la résistance est doublée?

3. Un filament de tube à vide reçoit un courant de 0,3 A pour une tension appliquée de 6,3 V.

(a) Dessiner le schéma en figurant le filament sous la forme d'une résistance,

(b) Quelle est la résistance du filament?

4. Transformer les unités suivantes en utilisant les puissances de 10 lorsque cela est nécessaire:

(a) 12 mA en ampères; (b) 5000 V en kilovolts; (c) 0,5 MΩ en ohms; (d) 100 000 ohms en mégohms; (e) 0,5 A en milliampères; (f) 9000 µS en siemens; (g) 1000 µA en milliampères; (h) 5 kΩ en ohms; (i) 8 nanosecondes (ns) en secondes.

5. Un courant de 2 A circule dans une résistance de 6 Ω branchée aux bornes d'une batterie,

(a) Quelle est la valeur de la tension de la batterie?

(b) Quelle est la puissance dissipée dans la résistance?

6. (a) Quelle est la valeur de la résistance permettant la circulation d'un courant de 30 A pour une tension de 6 V?

(b) Quelle est la valeur de la résistance permettant la circulation d'un courant de 1 mA pour une tension de 10 kV?

Pour quelle raison le courant en (b) est-il inférieur alors que la tension appliquée est plus grande?

7. Une source de tension produit un courant de 1 mA à travers une résistance de 10 MΩ. Quelle est la tension appliquée?

8. Calculer le courant en ampères dans les exemples suivants:

(a), 45 V aux bornes de 68 kΩ; (b) 250 V aux bornes de 10 MΩ; (c) 1200 W dissipés dans 600 Ω.

9. Calculer la tension IR dans les différents cas suivants:

(a) 68 µA dans 22 MΩ; (b) 2,3 mA dans 47 kΩ; (c) 237 A dans 0,012Ω.

10. Calculer la résistance R en ohms dans les différents cas suivants:

(a) 134 mA produit par 220 V; (b) 800 W dissipés pour une tension de 120 V; (c) une conductance de 9000 µS.

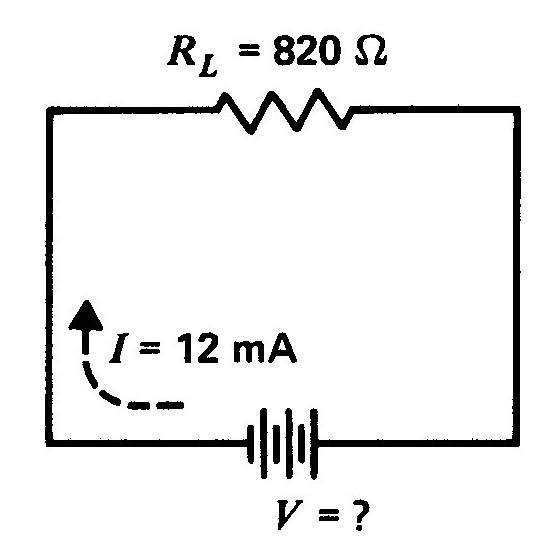
11. Calculer la valeur de V du circuit de la figure 2-7.

Figure 2-7 Pour le problème 11.

Réponses aux problèmes pratiques