Chapitre 3 - les circuits série

Chapitre 3 - les circuits série

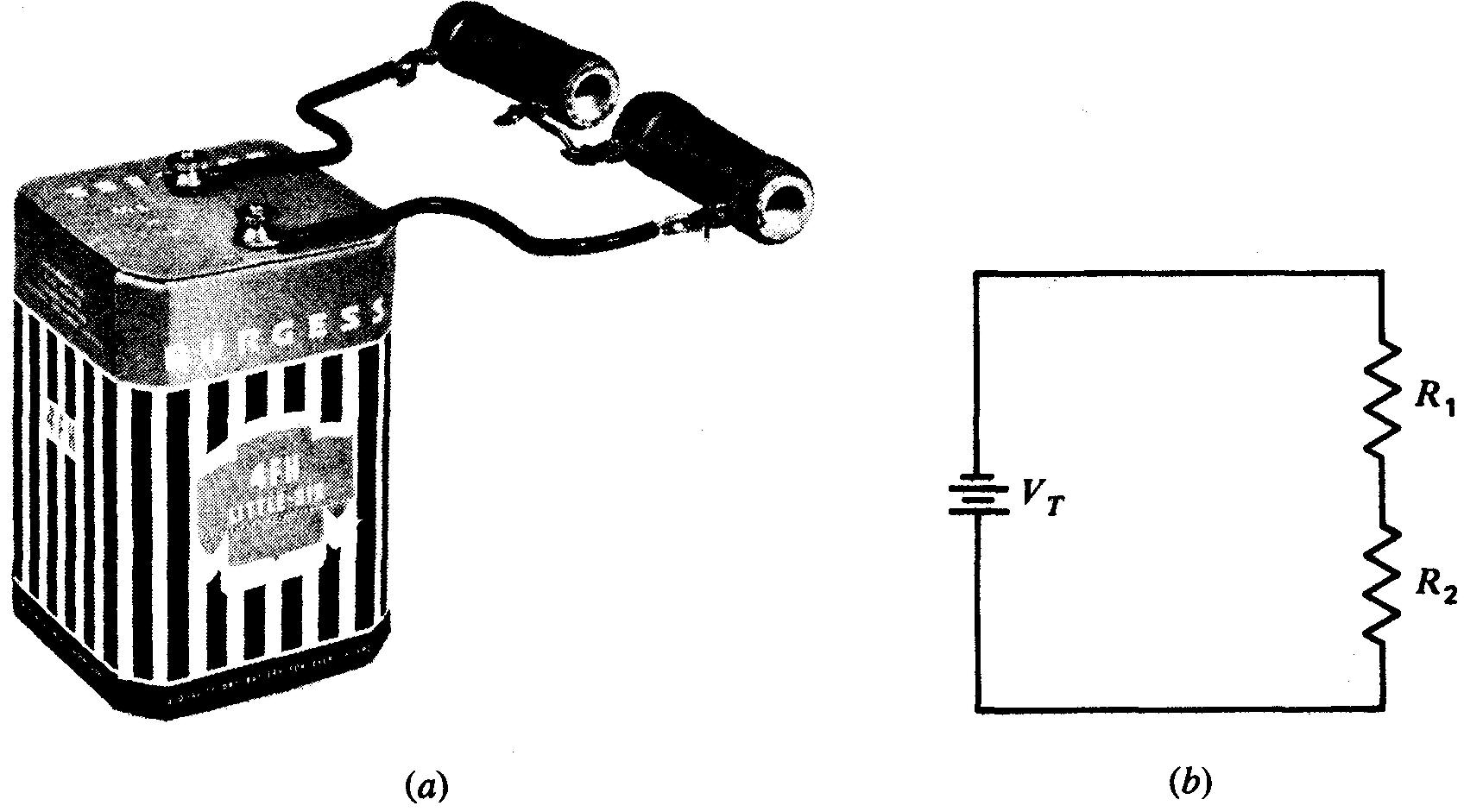
Quand les composants d'un circuit sont connectés par ordre successif, une extrémité de l'un étant reliée à une extrémité du suivant comme l'indique la figure 3-1, ils forment un circuit série.

Figure 3-1 Circuit série: (a) photographie du circuit câblé; (b) schéma.

Les résistances R1 et R2 sont en série l'une avec l'autre et en série avec la pile. Il n'y a donc qu'un seul passage pour la circulation des électrons.

Par conséquent, le courant I est le même pour tous les composants en série. Cette caractéristique ainsi que d'autres caractéristiques importantes sont étudiées dans les sections suivantes:

3.1 Pourquoi / est-il le même dans toutes les parties d'un circuit série?

3.2 La résistance totale R est égale à la somme de toutes les résistances en série

3.3 Les chutes de tension IR sont en série

3.4 La somme des chutes de tension IR en série est égale à la tension appliquée VT

3.5 Polarité des chutes de tension IR

3.6 Polarités par rapport à la masse du châssis

3.7 Puissance totale dans un circuit série

3.8 Tensions série en conjonction et tensions série en opposition

3.9 Étude des circuits série

3.10 Effet d'une coupure dans un circuit série

3.1 POURQUOI / EST-IL LE MÊME DANS TOUTES LES PARTIES D'UN CIRCUIT SÉRIE?

Un courant électrique est un mouvement de charges entre deux points; il est dû à la tension appliquée.

Sur la figure 3-2, la pile fournit la différence de potentiel qui force les électrons à se déplacer, de la borne négative A vers B, en suivant les fils de connexion et les résistances R1, R2 et R3, et à revenir à la borne positive J de la pile.

Figure 3-2 (a) Le déplacement d'électrons est le même en tous les points d'un circuit série; (b) le courant I est le même en tous les points d'un circuit série.

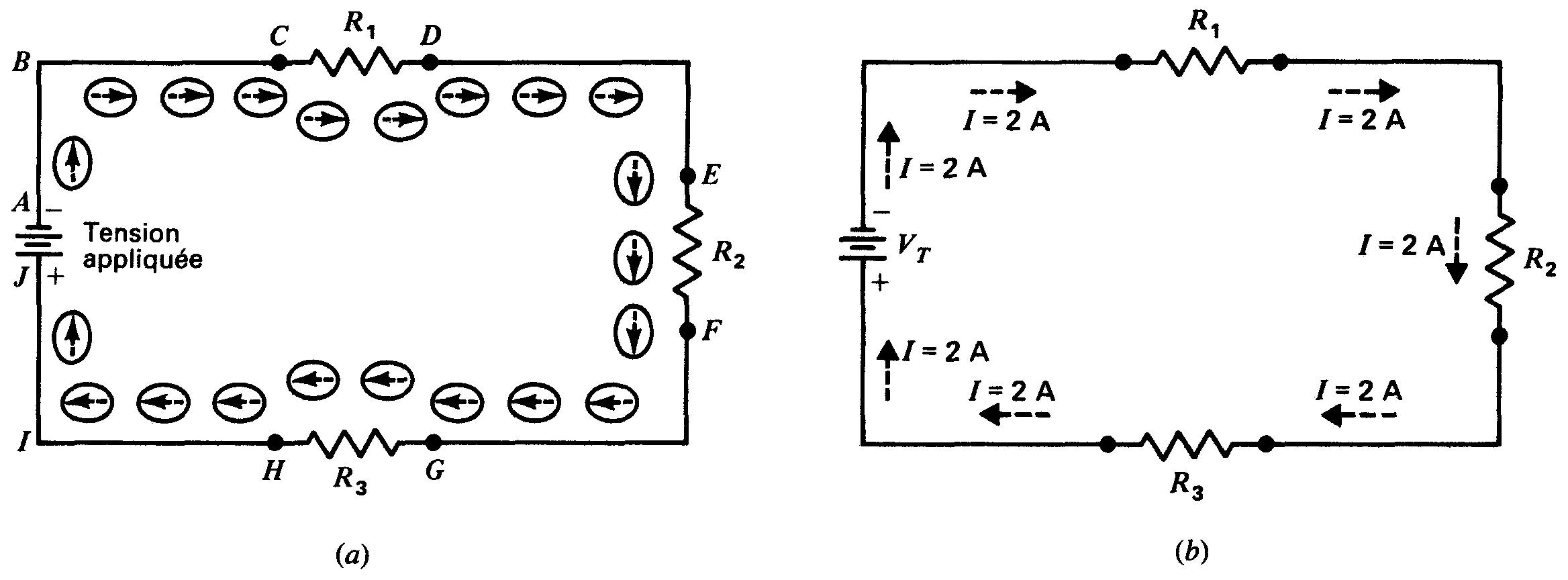
À la borne négative de la pile, la charge négative repousse les électrons. Les électrons libres des atomes du fil, à cette borne négative, sont repoussés de A vers B.

De même, les électrons libres, présents en B, peuvent repousser des électrons adjacents en créant un déplacement des électrons vers C dans la direction qui s'éloigne de la borne négative de la pile.

En même temps, la charge positive de la borne positive de la pile attire les électrons libres en les faisant se déplacer vers I et J. Par conséquent, les électrons libres des résistances R1, R2 et R3 sont forcés de se déplacer vers la borne positive.

La borne positive de la pile attire les électrons avec une force exactement égale à la force de répulsion exercée par le côté négatif de la pile.

Le mouvement des électrons libres commence donc en même temps et à la même vitesse dans toutes les parties du circuit.

Les électrons qui reviennent à la borne positive de la pile ne sont pas les mêmes que ceux qui quittent la borne négative, mais sont des électrons libres, forcés de se déplacer dans le fil jusqu'à la borne positive par la différence de potentiel de la pile.

Les électrons libres s'écartant d'un point sont remplacés en permanence par des électrons libres venant d'un point adjacent du circuit série. Tous les électrons ont la même vitesse que ceux qui quittent la pile.

Le déplacement des électrons est donc le même dans toutes les parties du circuit, le même nombre d'électrons se déplaçant, à un instant donné, à la même vitesse. C'est pourquoi le courant est le même dans toutes les parties du circuit série.

Par exemple, si le courant de la figure 3-2b est de 2 A, le courant qui traverse R1, R2 et R3 et la pile est aussi de 2 A.

Non seulement la valeur du courant est la même d'un bout à l'autre du circuit, mais le courant traversant toutes les parties d'un circuit série ne peut varier en aucune façon, puisqu'il n'y a qu'un seul trajet du courant pour tout le circuit.

L'ordre dans lequel on connecte les composants dans un circuit série n'a aucune influence sur le courant.

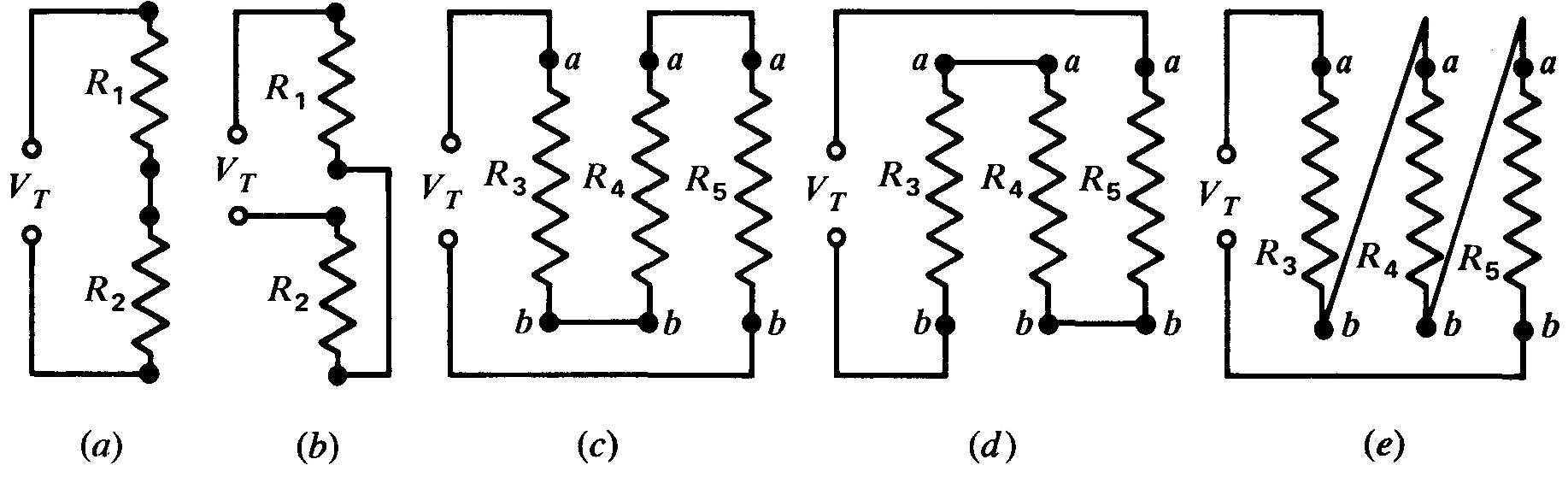
Sur la figure 3-3b, les résistances R1 et R2 sont inversées par rapport à la figure 3-3a, mais elles sont en série dans les deux cas et sont traversées par le même courant puisqu'il n'y a qu'un seul passage pour la circulation des électrons.

De même, R3, R4 et R5 sont en série et sont traversées par le même courant pour les connexions des figures 3-3c, d et e. Ces résistances ne sont pas obligatoirement égales.

Figure 3-3 Montages série: R1 et R2 sont en série en (a) et (b); R3, R4 et R5 sont en série en (c), (d) et (e).

Qu'un composant soit le premier, le second ou le dernier dans un circuit série n'a aucune importance pour le courant, puisque I a la même valeur, à un instant donné, dans tous les composants série.

De fait, on peut définir les composants en série comme étant des composants disposés sur le même chemin du courant.

Ce chemin va d'un côté de la source de tension, traverse les composants en série et rejoint l'autre côté de la source de la tension appliquée.

Ce chemin série ne doit comporter aucun point de dérivation du courant.

Cette caractéristique des circuits série s'applique non seulement au courant continu, mais aussi au courant alternatif quelles que soient sa fréquence et sa forme d'onde.

Problèmes pratiques 3.1 (réponses à la fin du chapitre)

(a) Considérer la figure 3-2. Nommer cinq parties de ce circuit série parcourues par le courant I de 2 A.

(b) Soit la figure 3-3e. Si I dans R5 est de 5 A, alors I dans R3 est de ??? A.

3.2 LA RÉSISTANCE TOTALE R EST ÉGALE À LA SOMME DE TOUTES LES RÉSISTANCES EN SÉRIE

Quand un circuit série est connecté aux bornes d'une source de tension, comme l'indique la figure 3-3, les électrons libres constituant le courant doivent se déplacer dans toutes les résistances série.

Ce passage est la seule voie que peuvent suivre les électrons pour revenir à la pile.

S'il y a deux résistances ou plus sur le même passage du courant, la résistance totale aux bornes de la source représente l'opposition exercée par toutes les résistances.

Plus précisément, la résistance totale (RT), d'une alignée de résistances est égale à la somme des résistances individuelles. La figure 3-4 illustre cette règle.

Figure 3-4 Des résistances en série s'additionnent: (a) la résistance R1 seule est de 3 Ω; (b) R1 et R2 en série font un total de 5 Ω (c) la résistance totale RT entre P1 et P2 est équivalente à une seule résistance de 5 Ω entre P1 et P2.

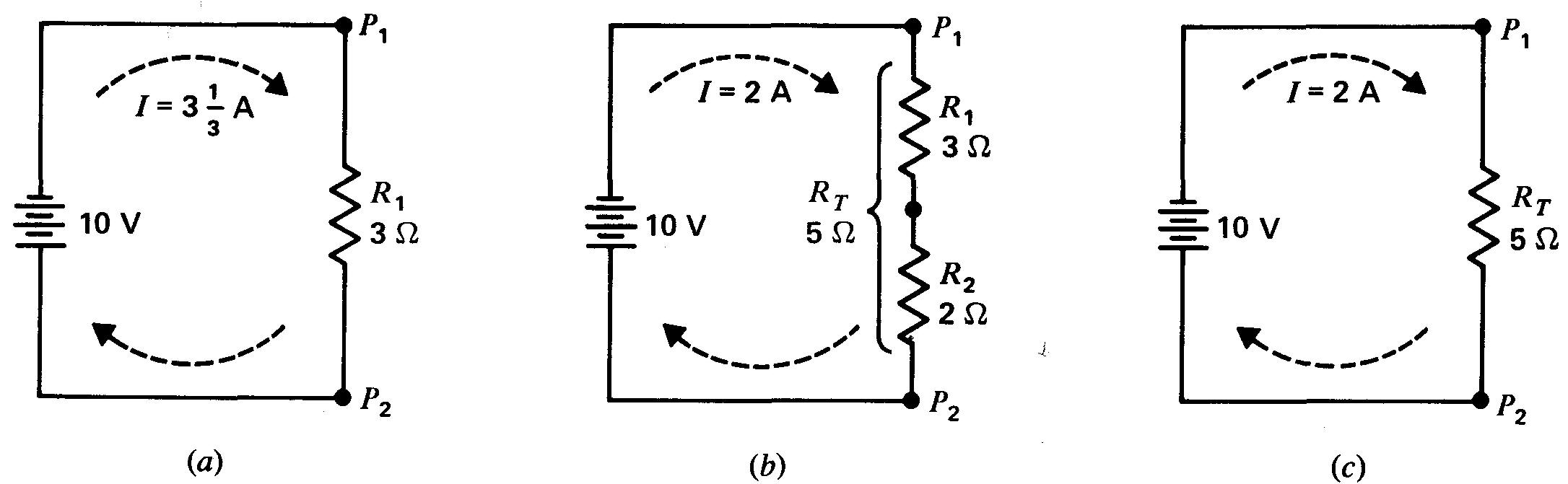
Sur la figure 3-4b, 2 Ω sont en série avec la résistance de 3 Ω de la figure 3-4a, pour former une résistance totale de 5 Ω.

L'opposition totale exercée par R1 et R2 pour limiter le courant est la même que si on avait utilisé une résistance de 5 Ω, comme l'indique le circuit équivalent de la figure 3-4c.

Chaîne série Une combinaison de résistances en série est souvent appelée une chaîne. La résistance d'une chaîne est égale à la somme des résistances individuelles.

Par exemple, R1 et R2 forment sur la figure 3-4 une chaîne résistances ayant une résistance totale de 5 Ω.

D'après la loi d'Ohm, le courant circulant entre deux points d'un circuit est égal au quotient de la différence de potentiel par la résistance entre ces points.

Comme toute la chaîne de résistances est connectée aux bornes de la source de tension, le courant est égal à la tension appliquée aux bornes de toute la chaîne divisée par la résistance totale de la chaîne.

Sur la figure 3-4, par exemple, 10 V sont appliqués, entre les points P1 et P2, aux bornes de 5 Ω, en (b) et (c) pour créer un courant de 2 A. Ce courant traverse R1 et R2.

Formule des résistances en série

En résumé, la résistance totale de la chaîne totale de résistances est égale à la somme des résistances individuelles.

La formule est:

RT = R1 + R2 + R3 + ... Rn (3.1)

où RT est la résistance totale et R1, R2, R3 et Rn sont les résistances en série individuelles.

Cette formule s'applique à un nombre quelconque de résistances, qu'elles soient égales ou non, pourvu qu'elles soient en série dans la même chaîne.

Remarquons que RT est la résistance à utiliser pour calculer le courant traversant la chaîne de résistances.

La loi d'Ohm s'écrit donc:

I = VT / RT

où RT est la somme de toutes les résistances, VT est la tension appliquée aux bornes de la résistance totale, et I, le courant traversant toutes les parties de la chaîne.

Exemple 1

Deux résistances R1 et R2 de 5 Ω chacune et une résistance R3 de 10 Ω sont montées en série.

Quelle est la valeur de Rt?

Réponse

RT = R1 + R2 + R3 = 5 + 5 +10

RT= 20Ω

Exemple 2

Si on applique 80 V aux bornes de la série de résistances de l'exemple 1, quel est le courant qui traverse R3?

Réponse

I = VT / RT = 80V / 20Ω = 4A

Ce courant de 4 A est le même dans R3, R2, R1 ou dans une partie quelconque du circuit série.

Remarquons qu'en ajoutant une résistance en série, on réduit le courant.

Sur la figure 3-4a, la résistance R1 de 3 Ω permet à la tension de 10 V d'établir un courant de 3,33 A.

Mais I est réduit à 2 A, quand on ajoute la résistance R2 de 2 Ω, ce qui porte à 5 Ω la résistance en série totale qui s'oppose à la source de 10 V.

Problèmes pratiques 3.2 (réponses à la fin du chapitre)

(a) V= 10 V, /R1 = 5 KΩ Calculer I.

(b) R2 = 2 kΩ et R3 = 3 kΩ sont disposées en série avec R1. Calculer RT.

3.3 LES CHUTES DE TENSION IR SONT EN SÉRIE

Selon la loi d'Ohm, si un courant traverse une résistance, il s'établit aux bornes de cette résistance une tension égale à I-R.

La figure 3-5 illustre cette loi.

Figure 3-5 Chutes de tension IR dans un circuit série.

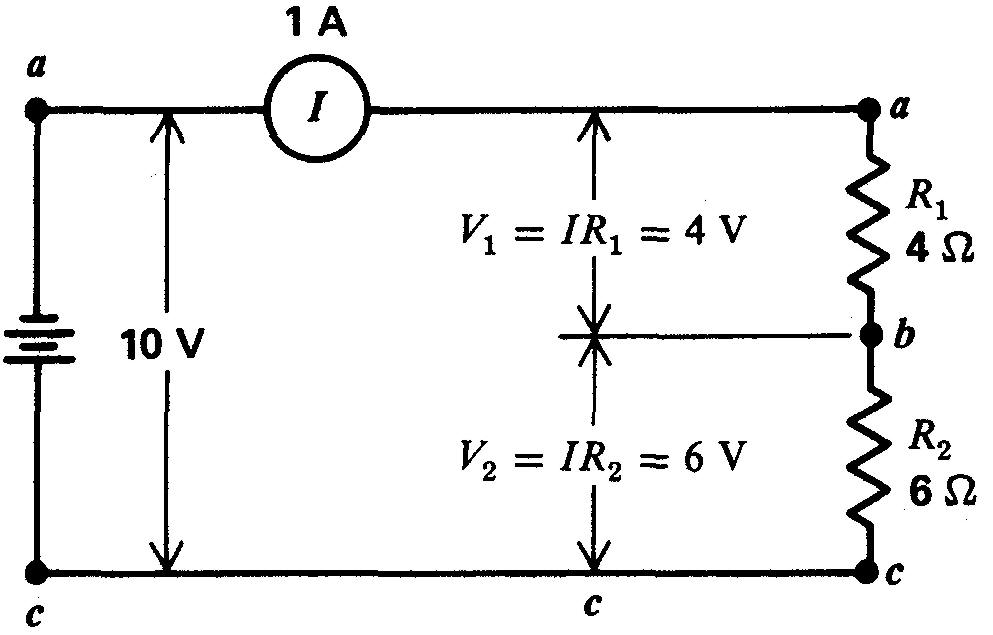
Dans ce cas, un courant de 1 A traverse les résistances en série R1 de 4Ω et R2 de 6 Ω. La résistance totale RT de 10 Ω est placée entre les bornes de la tension de 10 V appliquée.

Il en résulte une tension IR de 4 V égale à 1 A x 4 Ω aux bornes de R1 et une tension IR de 6 V égale à 1A x 6Ω aux bornes de R2.

La tension IR aux bornes de chaque résistance est appelée chute de tension IR, ou simplement chute de tension, car elle diminue la différence de potentiel disponible pour les autres résistances du circuit série.

Remarquons que l'on utilise les symboles V1 et V2 pour désigner les chutes de tension aux bornes de chaque résistance afin de les distinguer de la tension VT de la source appliquée aux deux résistances.

Notons que, sur la figure 3-5, la tension VT de 10 V est appliquée aux bornes de la résistance en série totale formée de R1 et R2.

Mais comme la chute de tension IR dans R1 est de 4 V, la différence de potentiel aux bornes de R2 est de 6 V seulement.

Le potentiel négatif tombe de 10 V au point a par rapport au point commun de référence c, jusqu'à 6 V au point b. La différence de potentiel de 6 V entre b et la référence en c est la tension aux bornes de R2.

Il y a, de la même manière, une chute de tension IR de 6 V aux bornes de R2.

Le potentiel négatif tombe de 6 V au point b, par rapport au point c, à 0 V au point c par rapport à lui-même.

La différence de potentiel entre deux points quelconques de la ligne de retour à la pile doit être nulle puisque le fil a une résistance pratiquement nulle et qu'il n'y a donc aucune chute de tension IR.

Il faut remarquer qu'on doit appliquer une tension provenant d'une source de différence de potentiel comme une pile pour qu'un courant s'établisse et qu'une chute de tension IR apparaisse aux bornes de la résistance.

Si aucun courant ne traverse une résistance, seule la résistance subsiste, mais il n'y a pas de différence de potentiel entre ses deux extrémités.

La chute de tension IR de 4 V aux bornes de R1, sur la figure 3-5, représente la portion de la tension appliquée utilisée pour établir un courant de 1 A dans la résistance de 4 Ω.

La chute de tension IR aux bornes de R2 est de 6 V, parce qu'il faut une différence de potentiel plus grande pour établir le même courant dans une résistance plus élevée.

En général, dans les circuits série, plus une résistance R est élevée, plus grande sera sa chute de tension IR.

Problèmes pratiques 3.3 (réponses à la fin du chapitre)

Considérer la figure 3.5:

(a) Calculer la somme V1 + V2;

(b) Calculer / selon le rapport VT/RT ;

(d) Calculer le courant / circulant dans R2.

3.4 LA SOMME DES CHUTES DE TENSION IR EN SÉRIE EST ÉGALE À LA TENSION APPLIQUÉE VT

Toute la tension appliquée est égale à la somme de ses parties.

Sur la figure 3-5, par exemple, les chutes de tension individuelles de 4 V et de 6 V forment au total la même tension de 10 V appliquée par la pile.

On peut énoncer cette relation pour les circuits série sous la forme:

VT = V1 + V2 + V3 + ... Vn (3.3)

où VT est la tension appliquée qui est égale à la somme des chutes de tension IR individuelles.

Exemple 3

Une source de tension produit une chute de tension IR de 40 V aux bornes d'une résistance R1 de 20 Ω, de 60 V aux bornes d'une résistance R2 de 30 Ω et de 180 V aux bornes d'une résistance R3 de 90 Ω, toutes en série.

Quelle est la tension appliquée?

Réponse

VT = 40V + 60V + 180V

VT = 280V

Remarquons que la chute de tension IR aux bornes de chaque résistance R est due au même courant de 2 A, établi par la tension de 280 V aux bornes de la résistance totale RT de 140 Ω.

Exemple 4

Une tension appliquée VT de 120 V produit des chutes de tension IR aux bornes de deux résistances en série R1 et R2.

Si la tension aux bornes de R1 est de 40 V, quelle est la chute de tension aux bornes de R2?

Réponse

Puisque V1 et V2 doivent faire au total 120 V, comme l'une est égale à 40 V, l'autre doit être égale à la différence entre 120 V et 40 V.

C'est-à-dire que V2 = VT-V1, ou 120 - 40. Donc V2 = 80V.

Il est bien normal que VT soit la somme des chutes de tension IR en série.

Le courant I est le même dans tous les composants en série. La somme de toutes les tensions en série est nécessaire à la création du même courant I dans l'ensemble de toutes les résistances en série puisque chaque tension aux bornes de chaque résistance R produit dans R ce courant I.

Chaîne de filaments en série d'un téléviseur

La figure 3-6 illustre une application classique des circuits série.

Figure 3-6 Chaîne typique des filaments en série des tubes d'un téléviseur.

C'est un exemple typique de circuit de filaments des téléviseurs noir et blanc à tubes.

Tous ces filaments, y compris celui du tube image, constituent une chaîne série. Le courant de chauffage est un courant alternatif tiré du secteur alternatif.

Les formules des composants en série, cependant, sont les mêmes dans les circuits ca (à courant alternatif), AC (alternative current) que dans les circuits ce (à courant continu).

Les premiers chiffres du numéro du tube donne la tension à appliquer au filament pour obtenir le courant de chauffage requis.

Le tube amplificateur 17BF11, par exemple, nécessite une tension de 17 V aux bornes des deux broches du filament pour que ce dernier soit parcouru par un courant de 450 mA.

Pour les tubes image, cependant, les premiers chiffres donnent la dimension de l'écran.

Le tube image 16CWP4, par exemple, a un écran de 16 pouces (406 mm), distance mesurée diagonalement entre les coins opposés. P4 désigne le numéro du phosphore d'un écran blanc; P22 précise les phosphores rouge, vert et bleu des téléviseurs couleur.

La tension de filament de la plupart des tubes image est de 6,3 V.

Chaque filament exige donc une tension inférieure aux 120 V offerts par le secteur.

Par contre tous réclament, en fonctionnement normal, le même courant. Les filaments sont donc connectés en une chaîne série aux bornes de la source de tension.

L'idée sous-jacente à ce branchement série est d'égaler à peu de chose près la somme des chutes de tension IR en série à la tension du secteur.

L'addition des tensions du circuit de la figure 3-6, soit 17 + 33 + 23 + 15 + 11+8 + 6,3 + 3 + 6,3 donne 122,6 V, légèrement plus que les 120 V du secteur.

Tout filament dispose d'une partie proportionnelle de la tension appliquée. Cette partie de la tension appliquée, déterminée par la résistance du filament est la valeur que ce dernier requiert.

Le circuit série, cependant, fournit le même courant à tous les filaments.

Les tubes conçus pour les chaînes série ont tous le même courant nominal, mais ceux réclamant le plus de puissance disposent d'une tension plus élevée.

La raison pour laquelle les tensions de la chaîne sont différentes réside dans le fait que les filaments à résistance plus élevée présentent une chute de tension IR plus grande.

Comment les circuits série sont utilisés Le circuit de la figure 3-6 est un exemple de montage série de composants réclamant tous le même courant, mais de tension nominale inférieure à celle de la source.

Dans un tel cas, la valeur de la tension appliquée VT est assez grande pour fournir le courant I requis par la résistance totale Rt.

Rappelons-nous que la tension VT est appliquée aux bornes de RT et non aux bornes de chaque résistance R individuelle.

Si l'on utilise une seule résistance R pour calculer I, alors il faut considérer la chute de tension individuelle aux bornes de ce composant. La valeur V/R pour chaque composant est égale à I calculé par la formule VT/RT pour le circuit série entier.

Cas d'une chute IR nulle Souvenons-nous que le produit IR est nul lorsque soit I, soit R est nul.

Le conducteur de connexion a une résistance R pratiquement nulle. La chute de tension IR aux bornes des fils d'interconnexion est donc pratiquement nulle; même lorsque le courant normal y circule.

La seconde possibilité est d'avoir une résistance, mais pas de courant.

Alors, soit la tension à appliquer est débranchée, soit le circuit est ouvert. Une résistance comporte en elle-même sa propre valeur, mais elle ne présentera aucune chute de tension IR si aucun courant ne la traverse.

Problèmes pratiques 3.4 (réponses à la fin du chapitre)

(a) Un circuit série présente des chutes IR de 10, 20 et 30 V. Calculer la tension de la source VT appliquée.

(b) Une tension de 100 V est appliquée aux résistances en série R1 et R2. V1 = 25 V. Calculer V2.

3.5 POLARITÉ DES CHUTES DE TENSION IR

Quand une chute de tension IR se produit dans une résistance, une des extrémités doit être plus positive ou plus négative que l'autre.

Sinon, sans différence de potentiel, il ne pourrait pas y avoir de courant dans la résistance pour produire la chute IR.

On peut associer la polarité de cette chute IR au sens de la circulation de I dans R.

En bref, les électrons pénètrent dans le côté négatif de la tension IR et sortent du côté positif (figure 3-7a).

Figure 3-7 Polarité des chutes de tension IR:

(a) les électrons entrent dans le côté négatif; (b) même polarité, avec des charges positives entrant du côté positif.

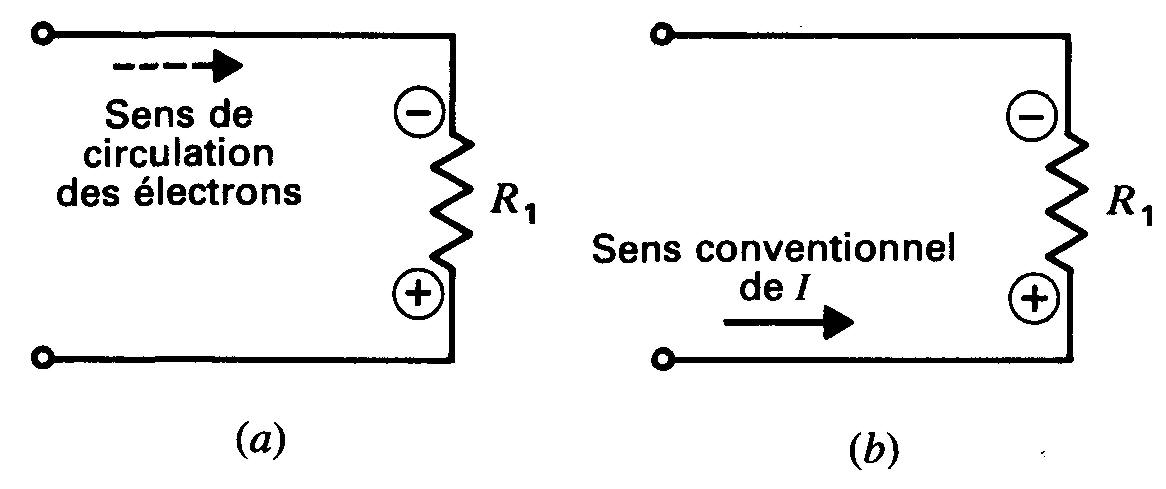
Si l'on désire considérer le courant conventionnel avec les charges se déplaçant dans le sens opposé à celui des électrons, il suffit d'inverser la règle et d'envisager les charges positives.

Voir la figure 3-7b, les charges positives constituant I entrent dans le côté positif de la tension IR.

Que l'on considère le sens de circulation des électrons ou le sens conventionnel, la polarité réelle de la chute de tension IR reste la même.

Dans les deux illustrations a et b de la figure 3-7, les extrémités supérieures de R de ces illustrations sont négatives puisqu'elles se confondent avec la borne négative de la source produisant le courant. Après tout, la résistance ignore le sens du courant dont nous parlons.

La figure 3-8 représente un circuit série à deux chutes de tension IR. Analysons ces polarités en considérant le sens de circulation des électrons.

Figure 3-8 Deux chutes de tension IR en série. Le sens de circulation des électrons indique le sens de I.

Les électrons se déplacent de la borne négative de la source VT et traversent R1 de c vers d. Les électrons pénètrent en c et sortent en d. Par conséquent, c est le côté négatif de la chute de tension aux bornes de R1.

De la même façon, pour la chute de tension IR aux bornes de R2, le point e est le côté négatif par rapport au point I.

Une méthode plus théorique de considérer la polarité des chutes de tension IR dans un circuit consiste à dire qu'entre deux points quelconques, le plus proche de la borne positive de la source est plus positif; le point le plus proche de la borne négative de la tension appliquée est aussi le plus négatif.

Un point plus proche d'une borne signifie que la résistance qui le sépare de cette borne est plus faible.

Sur la figure 3-8, le point c est plus proche de la borne négative de la pile que le point d, puisqu'il n'y a pas de résistance entre c et a, tandis que le trajet allant de d à a comprend la résistance R1.

De même, le point f est plus proche de la borne positive de la pile que le point e, ce qui rend f plus positif que e.

Remarquons que les points d et e de la figure 3-8 sont marqués avec les polarités plus et moins. La polarité plus, en d, indique que d est plus positif que le point c.

Mais cette polarité n'est indiquée que pour la tension aux bornes de R1 Le point d ne peut pas être plus positif que les points f et b. La borne positive de la tension appliquée doit être le point le plus positif puisque la pile génère le potentiel positif pour tout le circuit.

De même, les points a et c doivent avoir le potentiel le plus négatif de tout le montage en série, puisque ces points sont la borne négative de la tension appliquée.

En réalité, la polarité marquée plus, en d, signifie seulement que cette extrémité de R1 est moins négative que c, d'une quantité égale à la chute de tension dans R1.

Considérons la différence de potentiel entre e et d, sur la figure 3-8; le chemin entre ces points est seulement un morceau de conducteur.

Cette tension est nulle parce qu'il n'y a pas de résistance entre ces deux points. Comme il n'y a pas de résistance à cet endroit, le courant ne peut pas créer la chute de tension IR nécessaire pour former une différence de potentiel.

Les points e et d sont donc identiques du point de vue électrique puisqu'ils ont le même potentiel.

Quand nous tournons autour du circuit extérieur, à partir de la borne négative de VT, dans le sens de la circulation des électrons, les chutes de tension sont des chutes de potentiel négatif.

Dans la direction opposée, en partant de la borne positive de VT, les chutes de tension sont des chutes de potentiel positif.

Dans l'un ou l'autre cas, la chute de tension de chaque R en série correspond à la proportion de VT nécessaire pour l'unique valeur de courant qui circule dans toutes les résistances.

Problèmes pratiques 3.5 (réponses à la fin du chapitre)

Se reporter à la figure 3-8:

(a) Quel point de ce circuit est le plus négatif?

(b) Quel point de ce circuit est le plus positif?

3.6 POLARITÉS PAR RAPPORT À LA MASSE DU CHÂSSIS

Dans les circuits pratiques, un côté de la source de tension VT est habituellement connecté à la masse. Et ce, dans le but de simplifier le câblage.

Le cordon de soudure, le long du bord d'une plaquette de plastique à câblage imprimé, sert de mise à la masse, comme l'illustre la figure 3-9a.

Figure 3-9 Polarité des chutes de tension IR par rapport, à la masse du châssis:

(a) schéma de câblage avec le câblage de masse autour de la plaquette à circuit imprimé;

(b) schéma avec VT = +20 V par rapport à la masse du châssis;

Dans ce cas, une seule borne de la tension de source VT sert de côté haut du câblage. Les composants du circuit ont des connexions de retour au côté opposé de VT à travers la masse du châssis conducteur.

La borne négative ou la borne positive de VT peut être connectée à la ligne de retour de la masse du châssis. Le côté négatif étant mis à la masse, VT fournit la tension positive pour le côté haut du circuit (figure 3-9b).

Dans le cas de la figure 3-9c, le côté haut du châssis présente une tension négative par rapport à la masse du châssis.

Les deux résistances égales du circuit de la figure 3-9 partagent la tension appliquée en deux parties égales.

Les résistances R1 et R2 ont donc chacune une chute de tension de 10 V, soit la moitié des 20 V de VT. La somme des chutes IR est de 10 + 10 = 20 V, soit la tension appliquée totale.

Tensions positives par rapport à la masse

Le point S de la figure 3-9b est à + 20 V. Le point J, à la jonction de R1 et R2, est cependant à +10 V.

Le potentiel de +10 V est de 10 V inférieur à celui à S, à cause de la chute de 10 V dans R1. Toutes ces tensions sont positives par rapport à la masse du châssis, car le côté négatif de VT et le retour par la masse sont en réalité confondus.

Tensions négatives par rapport à la niasse

Le circuit de la figure 3-9c est identique à celui de (b), avec toutefois des tensions négatives au lieu de tensions positives. Le point S est à - 20 V, puisque le côté positif de la tension de la source est mis à la masse.

Problèmes pratiques 3.6 (réponses à la fin du chapitre)

(a) Soit le circuit de la figure 3-9b.

Donner, par rapport à la masse, la tension des points S, J et G.

(b) Soit le circuit de la figure 3-9c. Donner la tension, par rapport à la masse, des points S, J et G.

3.7 PUISSANCE TOTALE DANS UN CIRCUIT SÉRIE

La puissance utilisée pour créer un courant dans chaque résistance en série se dissipe sous forme de chaleur.

La puissance totale utilisée est donc la somme des valeurs individuelles de puissance dissipées dans chaque partie du circuit selon la formule:

PT= P1 +P2 + P3 + ... Pn (3.4)

Sur la figure 3-10, R1 dissipe 40 W, soit 4 x 10 pour I²R, 20 x 2 pour VI, ou 400/10 pour V²/R.

Figure 3-10 La somme des puissances individuelles P1 et P2 utilisées dans chacune des résistances, est égale à la puissance totale Pt fournie par la source.

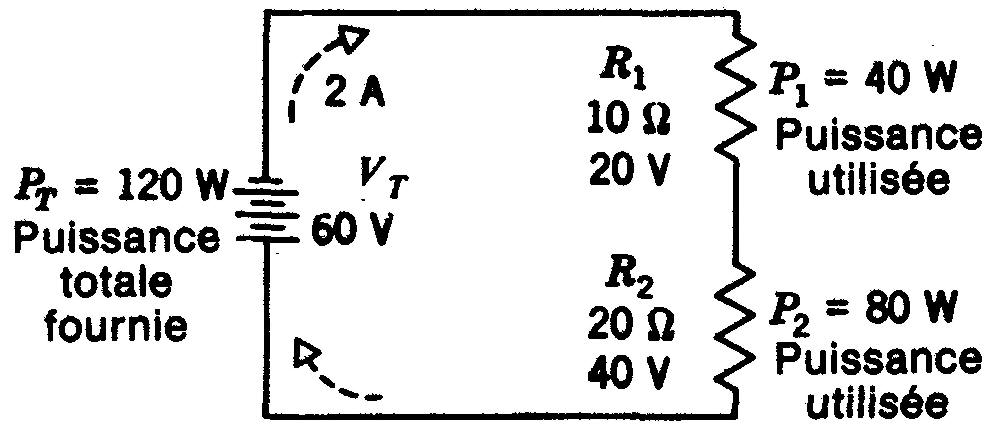
De même, la puissance dissipée dans R2 est égale à 80 W.

La puissance totale dissipée par R1 et R2 est donc 40 + 80, c'est-à-dire 120 W. Cette puissance est fournie par la source de tension appliquée.

On peut aussi calculer la puissance totale à partir de VTI, puisque la tension appliquée VT est la somme des tensions individuelles. Dans ce cas, PT=VTI = 2 x 60 = 120 W.

La puissance totale est donc de 120 W, calculée de l'une ou l'autre manière, puisque c'est la puissance délivrée par la pile. La source de tension produit une puissance égale à la puissance utilisée par la charge.

Problèmes pratiques 3.7 (réponses à la fin du chapitre)

(a) Trois résistances égales dissipent chacune 2 W. Calculer la puissance PT fournie par la source.

(b) Deux résistances série, R1 de 1 kΩ et R2 de 40 kΩ, sont branchées aux bornes d'une source de 50 V.

Déterminer laquelle de ces résistances dissipe la plus grande puissance.

3.8 TENSIONS SÉRIE EN CONJONCTION ET TENSIONS SÉRIE EN OPPOSITION

Les tensions séries en conjonction sont reliées de telle sorte que leurs polarités permettent la circulation du courant dans le même sens.

Considérons la figure 3-11a:

Figure 3-11 Tensions en série V1 et V2: (a) en conjonction; (b) en opposition.

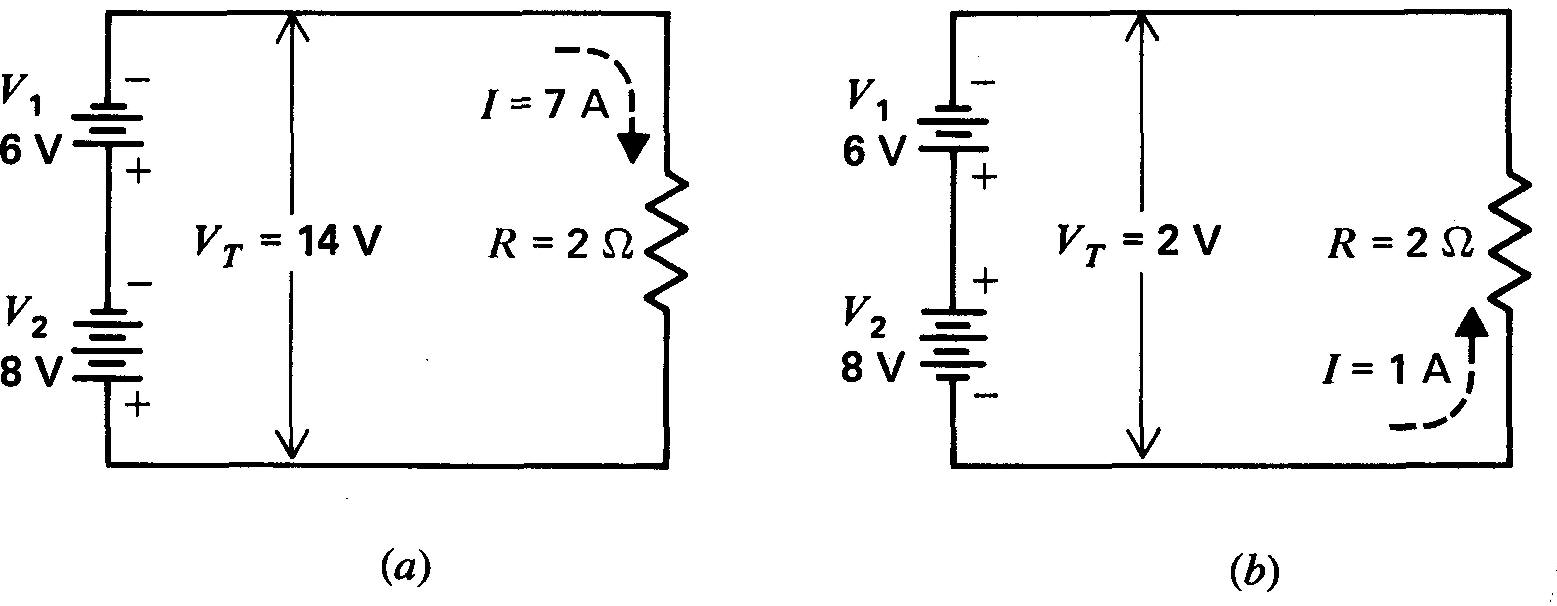
les 6 V seuls de V1 pourraient produire, selon R = 2 Ω, un débit d'électrons de 3 A à la sortie de la borne négative. De la même façon les 8 V de V2 pourraient produire 4 A dans le même sens. Le courant total est donc de 7 A.

Au lieu d'ajouter les courants, cependant, on pourrait additionner les tensions V1 et V2, ce qui donnerait une tension VT de 6 + 8 = 14 V. Cette tension produit, selon R = 2 Ω, un courant dans toutes les parties de 7 A.

Pour brancher des tensions en conjonction, relier la borne positive de l'une à la borne négative de la suivante.

La tension équivalente est la somme des tensions individuelles. Ce concept s'applique de la même façon, non seulement aux sources de tension comme les piles, mais également aux chutes de tension aux bornes des résistances.

On peut additionner n'importe quel nombre de tensions, à la condition qu'elles soient connectées en conjonction.

Les tensions en série en opposition se soustraient, comme le montre la figure 3-11b. Remarquons que les bornes positives de V1 et V2 sont reliées entre elles.

Soustraire la plus petite de la plus grande et attribuer à la tension nette VT ainsi obtenue la polarité de la plus grande. Dans l'exemple illustré, VT = 8 - 6 = 2 V. VT a même polarité que V2 puisque V2 est plus grand que V1.

Si deux tensions série en opposition sont égales, alors la tension nette est nulle. Dans ce cas, en effet, une tension équilibre l'autre. Le courant I est lui aussi nul, puisque la différence de potentiel nette est nulle.

Problèmes pratiques 3.8 (réponses à la fin du chapitre)

(a) Deux tensions en série, V1 de 40 V et V2 de 60 V, sont en conjonction série. Calculer VT.

(b) Ces mêmes tensions en série sont en opposition. Calculer VT.

3.9 ÉTUDE DES CIRCUITS SÉRIE

Considérons la figure 3-12.

Figure 3-12 Étude d'un circuit série pour trouver I, V1, V2, P1 et P2. Voir la solution dans le texte.

Supposons que la source VT de 50 V soit connue, que R1 soit de 14 Ω et R2 de 6Ω.

Le problème consiste à trouver RT, I, les chutes de tension individuelles V1 et V2 dans chaque résistance et la puissance dissipée.

Nous devons connaître la résistance RT pour calculer I puisque la tension totale appliquée, VT, est donnée. Cette tension VT est appliquée aux bornes de la résistance totale RT. Dans cet exemple, RT est de 14 + 6 = 20 Ω.

On peut maintenant calculer I = V/RT, ou 50/20, c'est-à-dire 2,5 A. Ce courant de 2,5 A circule dans R1 et R2.

Les chutes de tension individuelles sont:

V1 = IR1 = 2,5 x 14 = 35V

V2 = IR2 = 2,5 x 6 = 15V

Remarquons que la somme de V1 et V2 est égale à 50 V, c'est-à-dire à la tension appliquée VT.

Pour trouver la puissance dissipée dans chaque résistance, on calcule:

P1 = V1 x I = 35 x 2,5 = 87,5 W

P2 = V2 x I= 15 x 2,5 = 37,5 W

Ces deux valeurs de puissance dissipée font un total de 125 W.

La puissance délivrée par la source est égale à VT x I, soit 50 x 2,5, ce qui fait aussi 125 W.

Méthodes générales applicables aux circuits série

Pour résoudre les autres types de problèmes concernant les circuits série, il est utile de se rappeler ce qui suit:

1. Si on connaît I pour un composant, prendre ce I pour tous les composants puisque le courant est le même dans toutes les parties d'un circuit série.

2. Pour calculer I, on peut diviser la tension VT totale par la résistance totale, RT, ou bien une chute de tension individuelle IR par la R correspondante.

Par exemple, on pourrait calculer le courant de la figure 3-12 comme le quotient V2 / R2, soit 15/16, ce qui donne la même valeur de 2,5 A pour I.

Cependant, il ne faut pas confondre une valeur totale pour tout le circuit avec une valeur individuelle pour une partie du circuit seulement.

3. Si on connaît les chutes de tension individuelles le long du circuit, on peut les ajouter pour obtenir la tension totale VT.

Ceci montre que l'on peut aussi retrancher une chute de tension connue de la tension VT totale pour trouver la chute de tension restante.

Le problème de la figure 3-13 illustre ces principes.

Figure 3-13 Trouvez la résistance R3. Voir dans le texte l'étude de ce circuit série.

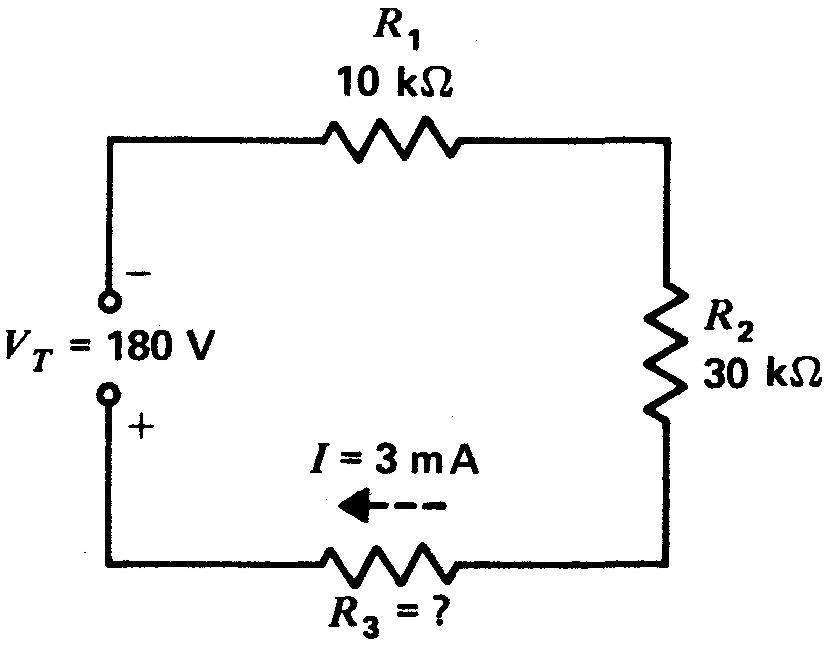
Dans ce circuit, on connaît Ri et R2 mais R3 est inconnu. Mais on donne le courant qui traverse R3, soit 3 mA.

On peut calculer toutes les grandeurs de ce circuit à partir de ces données seulement.

Le courant I de 3 mA est le même dans chacune des trois résistances série.

Par conséquent:

V1 = 3mA x 10kΩ = 30V

V2 = 3mA x 30kΩ = 90V

La somme de V1 et de V2 est 30 + 90 = 120 V. Cette somme ajoutée à V3 doit faire un total de 180 V. Si bien que V3 est égal à 180 - 120 = 60 V.

La tension V3 =IR3 étant égale à 60 V, R3 est donc égal à 60/0,003 soit 20 000 Ω ou 20 kΩ. La résistance totale du circuit est de 60 kΩ, dans laquelle circule donc un courant de 3 mA quand on applique une tension de 180 V.

Une autre méthode pour résoudre ce problème consiste à trouver RT d'abord.

On peut, à partir de la formule I = VT/RT, calculer RT = VT / I.

Avec un courant I de 3 mA et VT de 180 V, la valeur de RT doit être de 180 V / 3 mA = 60 kΩ.

Donc R3 est: 60 kΩ - 40 kΩ = = 20 kΩ.

Les puissances dissipées dans chacune des résistances sont de 90 mW dans R1, de 270 mW dans R2 et de 180 mW dans R3. La puissance totale est de 540 mW.

Les résistances en série réduisent la tension

Une application courante des circuits série consiste à utiliser une résistance pour abaisser la tension VT de la source à une valeur plus faible, comme l'indique la figure 3-14.

Figure 3-14 Résistance Rs montée en série pour abaisser une tension VT, de 12,6 V à 9 V, aux bornes de R1. Voir les calculs dans le texte.

Ici, la charge RL représente un récepteur à transistors qui fonctionne normalement avec une pile de 9 V. Lorsque le récepteur est en fonctionnement, le courant continu est de 18 m A dans la charge quand la tension de 9 V est appliquée.

Les conditions nécessaires sont donc: 18 mA sous 9 V.

Pour faire fonctionner ce récepteur avec une tension VT de 12,6 V, on intercale la résistance Rs série abaissant la tension en série pour créer une chute de tension Vs qui porte VL à 9 V.

La chute de tension dans Rs est la différence entre VL et la tension plus élevée VT.

La formule est:

VS = VT - VL

Vs = 12,6 - 9 = 3,6 V

En outre, cette chute de tension de 3,6 V doit être créée par un courant de 18 m A, puisque le courant est le même dans Rs et RL.

Donc, pour calculer Rs, on fait le quotient 3,6 V / 18 mA, ce qui fait 0,2 kΩ ou 200 Ω.

La puissance dissipée dans RL se calcule comme le produit VL x IL. Elle a pour valeur: 3,6 V x 18 mA, soit 64,8 mW.

Circuit à sources de tension en série

Considérer la figure 3-15.

Figure 3-15 Calculer I de ce circuit série à trois sources de tension. Voir la solution dans le texte.

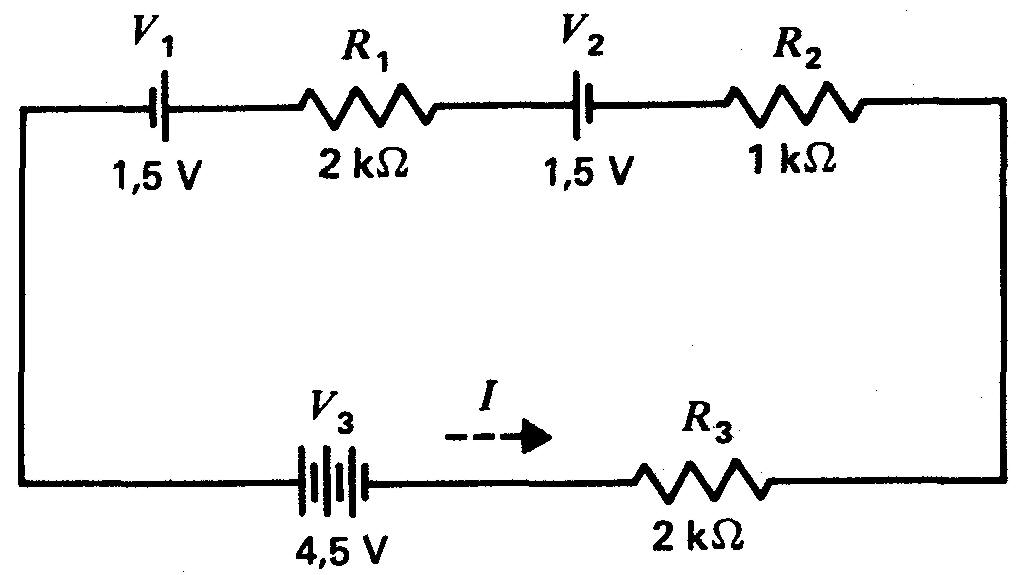
Remarquer que les tensions en série V1 et V2 sont en opposition avec les polarités de + à + via R1.

Leur effet net est de 0 V.

Par conséquent, VT est constitué de V3 seulement, d'où VT=4,5 V.

La résistance totale RT est égale à 2 +1 + 2 = 5 kΩ.

Finalement, I= VT / RT= 4,5 V /5 kΩ = 0,9 mA.

Problèmes pratiques 3.9 (réponses à la fin du chapitre) Considérer la figure 3-13:

(a) Calculer Vi aux bornes de R1,

(b) Calculer V2 aux bornes de R2;

3.10 EFFET D'UNE COUPURE DANS UN CIRCUIT SÉRIE

Une coupure est une rupture dans le passage du courant. La résistance de la coupure est très élevée, puisqu'un isolant comme de l'air prend la place d'un élément conducteur du circuit.

Comme le courant est identique dans toutes les parties d'un circuit en série, une coupure dans une partie quelconque d'un circuit se traduit par un courant nul dans tout le circuit.

Comme l'indique la figure 3-16, le circuit est normal en (a), mais en (b) il n'y a aucun courant ni dans R1, ni dans R2, ni dans R3, puisqu'il y a une coupure dans le circuit série.

Figure 3-16 Influence d'une coupure dans un circuit série:

(a) circuit normal fermé avec courant de 1 A;

(b) coupure en un point quelconque du circuit empêchant le passage d'un courant dans tout le circuit.

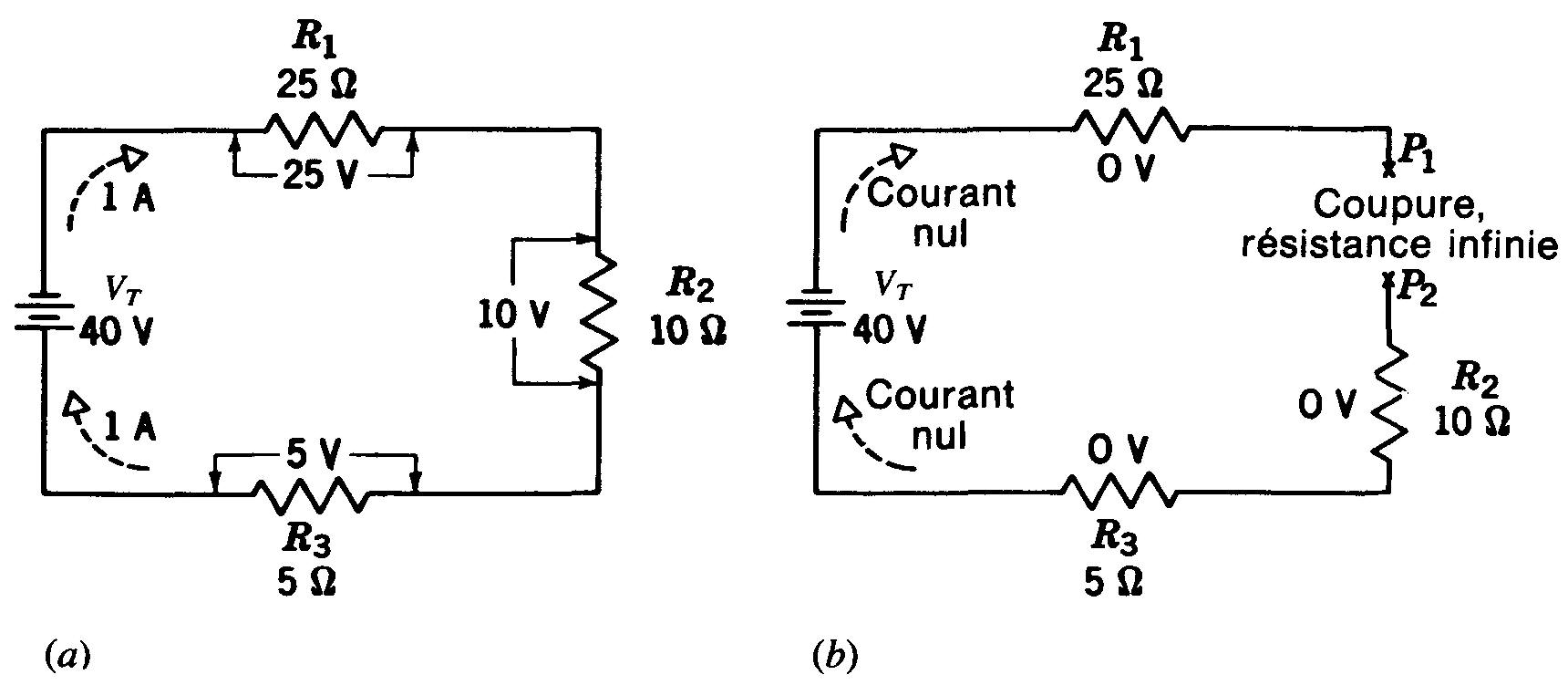
La coupure entre P1 et P2, ou en tout autre point du circuit, a une résistance pratiquement infinie étant donné que son opposition à la circulation d'électrons est très grande, comparée à la résistance de R1, R2 et R3.

Par conséquent, la valeur du courant est pratiquement nulle, bien que la pile délivre sa tension appliquée normale de 40 V.

Pour prendre un exemple, supposons que la coupure entre P1 et P2 ait une résistance de 40 000 000 000 Ω. La résistance de tout le circuit est pratiquement de 40 000 000 000 Ω, puisque l'on peut négliger la résistance de R1, R2 et R3 devant la résistance de la coupure.

Une si grande résistance est pratiquement une résistance infinie.

D'après la loi d'Ohm, le courant circulant quand on applique 40 V aux bornes de 40 000 000 000 Ω est de un milliardième d'ampère, ce qui est pratiquement nul.

C'est la valeur du courant dans toutes les parties du circuit série. Le courant étant pratiquement nul, la chute de tension IR est pratiquement égale à zéro aux bornes des 25 Ω de R1 des 10 Ω de R2 et des 5 Ω de R3.

En résumé, s'il y a une coupure dans une partie quelconque d'un circuit série, le courant est nul dans tout le circuit. Il n'y a aucune chute de tension IR dans aucune des résistances en série, bien que le générateur maintienne sa tension de sortie.

Cas d'une chute IR nulle

Considérer la figure 3-16b.

Chaque résistance du circuit ouvert présente une chute IR nulle. Cela est dû au fait que le courant est pratiquement nul dans tous les composants en série.

Chaque composant R cependant possède encore sa propre résistance. Cependant avec un tel courant nul les tensions IR sont nulles.

La source de tension VT est encore présente même si le courant I est nul.

Le circuit ouvert de la figure 3-16b illustre par un autre exemple la nature différente des grandeurs électriques V et I.

Il ne circule aucun courant dans un circuit ouvert, car le parcours extérieur entre les deux bornes de la pile n'est pas complet. Cependant, la pile génère encore une différence de potentiel entre ses bornes positive et négative.

Cette tension de source est présente qu'il y ait ou non un courant dans le circuit extérieur.

Si l'on mesure VT , l'appareil de mesure indiquera 40 V, que le circuit soit fermé ou ouvert.

Le même raisonnement est vrai pour une tension alternative de 120 V fournie par le secteur aux maisons. Cette différence de potentiel de 120 V est appliquée entre les deux bornes d'une prise murale.

Si l'on y branche une lampe ou un appareil électrique, le courant circulera dans le circuit. La différence de potentiel de 120 V sera toujours présente même si rien n'est connecté à la prise. Si l'on y touche, on ressentira une secousse électrique.

Le générateur de la centrale électrique maintient une source de 120 V aux prises pour produire un courant dans tous les circuits que l'on connecte.

La tension appliquée se retrouve entre les bornes de la coupure II importe de remarquer que toute la tension appliquée apparaît entre les bornes de la coupure du circuit.

Il existe entre Pi et P2 de la figure 3-16b une tension de 40 V car, essentiellement, toute la résistance du circuit série est entre P1 et P2. Par conséquent, la résistance de la coupure du circuit développe toute la chute de tension IR.

Le courant extrêmement petit d'un milliardième d'ampère n'est pas suffisamment fort pour développer une chute IR appréciable aux bornes de R1, R2 et R3.

Cependant, il y a aux bornes de la coupure1 une résistance de 40 GΩ (G = giga, milliard).

Par conséquent, la tension IR aux bornes de la partie ouverte est de un milliardième d'ampère multiplié par 40 GΩ, soit 40 V.

Nous pouvons aussi considérer le circuit ouvert comme un diviseur de tension proportionnel (voir le chapitre 6).

Comme pratiquement toute la résistance en série est entre P1 et P2, toute la tension appliquée se retrouve entre les bornes de la coupure.

Ce fait constitue un bon moyen de détection d'un composant ouvert dans une chaîne série. La mesure de la tension aux bornes d'un composant en bon état donnera 0 V.

Par contre, celui qui donne une lecture égale à la tension appliquée est ouvert.

Chaîne de filaments ouverte

Voir, en guise d'exemple, la chaîne de filaments d'un téléviseur à tubes illustrée à la figure 3-6.

Si un filament est coupé, la chaîne entière est ouverte.

Alors aucun des tubes, y compris le tube image, ne fonctionnera. Et l'on n'aura, en raison de cette petite panne que constitue un filament de chaîne coupé, ni son ni image.

Problèmes pratiques 3.10 (réponses à la fin du chapitre)

Considérer la figure 3-6:

(a) Quelle est la tension normale aux bornes du filament du tube 15BD11?

(b) Quelle est la tension aux bornes du filament du tube 15BD11 si le filament du 3GK5 est coupé?

La tension aux bornes d'un circuit ouvert est égale à la tension appliquée, même en l'absence totale de courant, quand la capacité entre les bornes de la coupure est chargée à la tension V, comme on l'indique au chapitre 21.

Résumé

1. Il n'y a qu'un seul courant I dans un circuit série. I = VT / RT, où VT est la tension appliquée aux bornes de la résistance en série totale RT. Ce courant I est le même dans tous les composants en série.

2. La résistance totale d'une chaîne en série est la somme des résistances individuelles.

3. La tension appliquée VT est égale à la somme des chutes de tension, IR, en série.

4. Le côté négatif d'une chute de tension IR est celui par lequel entrent les électrons qui sont attirés vers le côté positif à l'extrémité opposée.

5. La somme des valeurs individuelles des puissances utilisées dans les résistances individuelles est égale à la puissance totale fournie par la source.

6. Une coupure se traduit par un courant nul dans toutes les parties du circuit série.

7. Des tensions en série conjonction s'ajoutent; des tensions en série opposition se retranchent.

8. Dans un circuit ouvert, la tension entre les deux bornes de la coupure est égale à la tension appliquée.

Exercices de contrôle (Réponses aux exercices de contrôle)

Voici un moyen de contrôler si vous avez bien assimilé le contenu de ce chapitre. Ces exercices sont uniquement destinés à vous évaluer vous-même.

Choisir (a), (b), (c) ou (d).

1. Si deux résistances sont connectées en série:

(a) elles doivent avoir toutes deux la même valeur de résistance;

(b) la tension aux bornes de chacune d'elles doit être la même;

(d) il n'y a qu'un seul trajet possible pour le courant passant par toutes les résistances.

2. Sur la figure 3-3c, si le courant qui traverse R5 est de 1 A courant qui traverse R3 doit être de

(a) 0,33 A; (b) 0,5 A; (c)1 A; (d) 3 A.

3. Quand une résistance de 10 kΩ est en série avec une résistance de 2 Ω, la résistance totale est égale

à: (a) 2 kΩ; (b) 8 kΩ; (c) 10 kΩ; (d) 12 kΩ.

4. Si deux résistances égales sont montées en série aux bornes d'une batterie de 90 V, la tension, aux bornes de chaque résistance est égale à:

(a) 30 V; (b) 45 V; (c)90 V; (d) 180 V.

5. La somme des chutes de tension, IR, en série, est:

(a) inférieure à la plus faible chute de tension; (b) égale à la moyenne de toutes les chutes de tension;

6. Les résistances R1 et R2 sont en série et la tension appliquée est de 90 V. Si V1 est de 30 V, V2 doit donc être de:

(a) 30 V; (b) 90 V; (c) 45 V; (d) 60 V.

7. Une résistance de 4 Ω et une résistance de 2 Ω sont en série aux bornes d'une pile de 6 V.

Le courant: (a) dans la résistance la plus grande, est de 1,33 A; (b) dans la résistance la plus faible, est de 3 A;

8. Quand une résistance d'un montage série est ouverte:

(a) le courant est maximal dans les résistances normales; (b) le courant est nul dans toutes les résistances;

9. La résistance d'un montage série ouvert est:

(a) zéro; (b) infinie; (c) égale à la résistance normale du montage; (d) environ le double de la résistance normale du montage.

10. Une tension de 100 V est appliquée aux bornes d'une résistance R1 de 20 Ω et d'une résistance R2 de 30 Ω, montées en série. La tension V1 est égale à 40 V.

Le courant dans R2 est: (a) 5 A; (b) 3,33 A; (c) 1,33 A; (d) 2 A.

Questions

1. Montrer comment connecter deux résistances en série aux bornes d'une source de tension.

2. Énoncer trois règles concernant le courant, la tension et la résistance dans un circuit série.

3. Pour une valeur donnée du courant, pourquoi une résistance plus élevée crée-t-elle une chute de tension plus élevée entre ses bornes?

4. Deux lampes d'éclairage de 300 W, 120 V sont montées en série aux bornes d'une ligne de 240 V.

Si le filament de la première lampe se rompt, la seconde lampe éclairera-t-elle? Pourquoi?

Après cette rupture, quelle est la tension aux bornes de la source et aux bornes de chaque lampe?

5. Montrer que si VT = V1 + V2 + V3, on a RT = R1 + R2 + R3.

6. Énoncer brièvement une loi qui détermine la polarité de la chute de tension aux bornes de chacune des résistances d'un circuit série.

7. Retracer le circuit de la figure 3-13, en indiquant la polarité de V1, V2 et V3.

8. Énoncer brièvement une loi indiquant si des tensions en série sont en conjonction.

9. Établir la formule PT = P1+P2 + P3 à partir de VT = V1 + V2 + V3.

10. Pourquoi, dans une chaîne série, la plus grande résistance dissipe la plus grande puissance?

Problèmes (Réponses aux problèmes de numéro impair )

1. Dans un circuit, 10 V sont appliqués aux bornes d'une résistance R1 de 10 Ω.

Quel est le courant dans ce circuit?

Quelle résistance R2 faut-il mettre en série avec R1 pour réduire le courant de moitié?

Tracer le schéma du circuit avec R1 et R2.

2. Tracer le schéma des résistances de 20 Ω, 30 Ω et 40 Ω, en série,

(a) Quelle est la résistance totale du montage série?

(b) Quel est le courant qui circule dans chaque résistance du montage série si une tension de 180 V est appliquée aux bornes de la chaîne série?

(d) Trouver la puissance dissipée dans chaque résistance.

3. Deux résistances R1 de 90 kΩ et R2 de 10 kΩ sont en série aux bornes d'une source de 3 V.

(a) Tracer le schéma, (b) Quelle est la valeur de V2?

4. Tracer un schéma montrant deux résistances Ri et R2, en série, aux bornes d'une source de 100 V.

(a) Si la chute de tension dans R1 est de 60 V, quelle est la chute de tension IR dans R2?

(b) Marquer la polarité des chutes de tension dans R1 et dans R2.

(d) Quelle est la résistance de Ri et de R2?

Quelle est la résistance totale aux bornes de la source?

(e) Si on déconnecte la source de tension, quelle est la tension aux bornes de R1 et de R2?

5. Trois résistances de 10 Ω sont montées en série aux bornes d'une source de tension. Tracer le schéma.

Si la tension aux bornes de chaque résistance est de 10 V, quelle est la tension appliquée?

Quel est le courant dans chaque résistance?

6. Quelle résistance R1 faut-il mettre en série avec une résistance R2 de 100 Ω pour limiter le courant à 0,3 A, quand on applique 120 V?

Tracer le schéma.

Quelle est la puissance dissipée dans chaque résistance?

7. Quelle est la résistance totale RT équivalente aux résistances suivantes connectées en série:

2 MΩ; 0,5 MΩ; 47 kΩ; 5 kΩ; et 470 Ω.

8. En se reportant à la figure 3-6, calculer la résistance de chaque filament pour son courant normal de charge.

Quelle est la résistance totale du montage de filaments?

Quelle est la résistance avec un filament coupé?

9. Tracer le schéma de trois résistances égales montées en série aux bornes d'une source de 90 V, chaque résistance ayant à ses bornes le tiers de la tension appliquée, dans le cas où le courant du circuit est de 2 mA.

10. Une lampe de 100 W consomme normalement 0,833 A et une lampe de 200 W consomme 1,666 A quand elles sont alimentées sous 120 V.

Montrer que si on connectait ces deux lampes en série aux bornes de la source de 240 V, le courant I serait de 1,111 A dans les deux lampes en supposant que les résistances restent constantes.

11. Considérer la figure 3-9 et calculer le courant traversant les résistances R1 et R2 des circuits (a), (b) et (c) représentés.

12. Considérer la figure 3-17 et calculer I, V1, V2, P1, P2, et PT.

(Noter que R1 et R2 sont en série avec VT même si on a représenté la source à droite et non à gauche.)

13. Si on augmente R1 jusqu'à 8 kΩ, sur la figure 3-17, que deviendra le nouveau I ?

14. Trouver R1 sur la figure 3-18. Pourquoi I est-il dans le sens indiqué?

15. Trouver R2 sur la figure 3-19.

16. La figure 3-20 illustre le circuit de maintien à 12,6 V d'une batterie chargée par un générateur de 15 V.

Calculer I et indiquer le sens de déplacement des électrons.

17. Trouver V2, sur la figure 3-21. Indiquer les polarités de V1, V2 et V3.

18. Trouver VT, sur la figure 3-22. Indiquer les polarités de VT, V1 et V2

Réponses aux problèmes pratiques