Transformateurs

Électrotechnique

Voir aussi :

Expérience de Transformateur

Le transformateur est un appareil électrique très simple, mais il n'en constitue pas moins l'un des plus utiles. Le transformateur permet de modifier la tension et le courant dans un circuit.

Grâce à lui, l'énergie électrique peut être transportée à grande distance de façon économique et distribuée dans les usines et les maisons.

L'étude du transformateur nous aidera également à comprendre le fonctionnement d'un grand nombre de machines telles que moteurs d'induction, alternateurs, compensateurs synchrones, etc., car ces machines utilisent aussi le principe de l'induction électromagnétique.

C'est pourquoi nous recommandons au lecteur de porter une attention particulière à cette section.

Nous établirons d'abord quelques concepts de base, pour ensuite procéder à l'analyse du transformateur idéal. Connaissant les propriétés fondamentales du transformateur idéal, nous les appliquerons à l'étude des transformateurs utilisés en pratique.

Tension induite dans une bobine

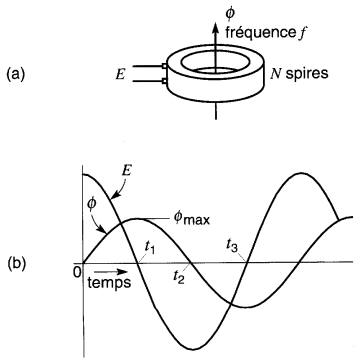
Soit une bobine entourant un flux qui varie sinusoïdalement à une fréquence f, atteignant périodiquement des crêtes positives et négatives de valeur Φ_max (Fig. 30-1).

Figure 30-1

a. Une tension alternative est induite aux bornes d'une bobine qui entoure un flux alternatif. b. Le flux sinusoïdal induit une tension sinusoïdale

Ce flux alternatif induit entre les bornes de la bobine une tension alternative donnée par l'équation:

E = 4,44 fΦ_max    (30-1)

où

E = tension efficace induite, en volts [V]

f = fréquence du flux, en hertz [Hz]

N = nombre de spires de la bobine

 Φ_max = valeur maximale du flux, en webers [Wb]

4,44 = constante (valeur exacte = π√2)

La provenance du flux n'a aucune importance ; il peut être créé par un enroulement extérieur, par un aimant en mouvement, ou par un courant qui circule dans la bobine elle-même.

Cette formule indique que pour une fréquence donnée la tension induite est proportionnelle au flux maximal Φ_max.

L'équation 30-1 découle de la loi de Faraday

E = NΔΦ / Δt,

où ΔΦ / Δt est le taux de changement du flux.

Ainsi, dans la Fig. 30-1b, durant l'intervalle de 0 à t i , ΔΦ / Δt est positif, donc la tension est positive.

De même, durant l'intervalle de t1 à t3, ΔΦ / Δt est négatif, donc la tension induite est négative.

Enfin, aux instants t1 et t3, ΔΦ / Δtt est nul, donc la tension est nulle.

Noter que ΔΦ / Δt est maximal aux moments où le flux 0 est nul. Or, c'est précisément à ces moments que la tension induite est maximale.

Exemple 30-1

Une bobine possédant 4000 spires entoure un flux sinusoïdal dont la valeur crête est de 2 milliwebers et la fréquence est 60 Hz.

Calculer la valeur de la tension induite.

Solution

On a:

E =  4,44 fΦ_max = 4,44 x 60 x 4000 x 0,002 = 2131 V

La tension efficace induite est de 2131 V, et sa valeur crête est 2131 √2 = 3014 V

Tension appliquée et tension induite

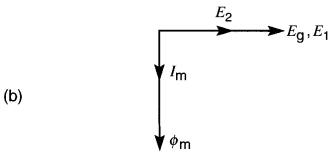
La Fig. 30-2a montre une bobine à noyau d'air raccordée à une source de tension sinusoïdale E_g.

Figure 30-2

a. La tension induite dans une bobine est égale à la tension appliquée. b. Diagramme vectoriel des grandeurs sinusoïdales

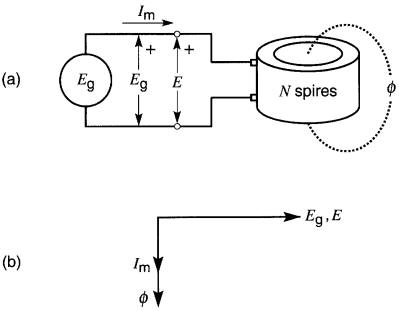
 Si la résistance de la bobine est négligeable, le courant vaut

I_m = E_glX_L

où X_L est la réactance inductive de l'enroulement.

Le flux créé par le courant alternatif induit aux bornes de la bobine une tension E dont la valeur est donnée par l'équation (30-1).

D'autre part, si l'on se réfère à la figure, on constate que la tension appliquée E_g et la tension induite E sont identiques car elles apparaissent entre les deux mêmes bornes.

Puisque E_g = E, on peut écrire:

E_g =  4,44 fΦ_max     (30-2)

d'où l'on tire:

Φ_max = E_g / 4,44fN

Pour une fréquence et un nombre de spires donnés, cette équation révèle que le flux 0max varie proportionnellement à la tension appliquée. De plus, si la tension E_g est constante, le flux maximal doit aussi demeurer constant.

Supposons, par exemple, qu'on introduise graduellement un noyau de fer à l'intérieur de la bobine tout en gardant la tension E_g de la source constante (Fig. 30-3).

Figure 30-3

a. Le flux demeure constant pendant que le noyau est introduit dans la bobine.

b. Diagramme vectoriel des grandeurs sinusoïdales. Le courant magnétisant est plus petit que dans la Fig. 30-2

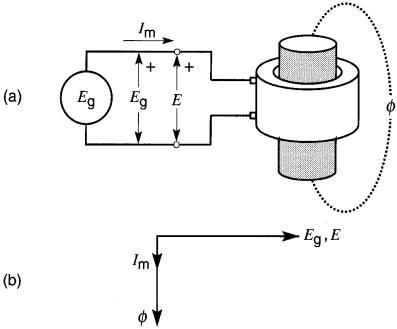
La valeur maximale du flux demeure rigoureusement constante pendant cette manoeuvre et, lorsque le noyau d'acier sera rentré complètement à l'intérieur de la bobine, le flux Φ_max n'aura pas changé.

En effet, si le flux augmentait (comme on pourrait le croire), la tension induite E augmenterait également.

Ceci est impossible car la tension E_g de la source demeure constante. Pour une même tension E_g, le flux dans les Fig. 30-2 et 30-3 reste donc le même. Cependant, le courant est beaucoup plus petit lorsque le noyau d'acier est à l'intérieur de l'enroulement.

En effet, pour produire le même flux avec un noyau de fer, on a besoin d'une FMM plus faible, donc d'un courant plus faible.

Ce courant I_m est appelé courant magnétisant; il est déphasé de 90° en arrière de la tension E_g, comme dans toute inductance (Fig. 30-2b et 30-3b).

 Exemple 30-2

Une bobine de 90 spires est raccordée à une source de 120 V, 60 Hz. Sachant que le courant magnétisant est de 4 A,

calculer :

a) la valeur crête du flux

b) la valeur crête de la FMM développée par la bobine

c) la réactance inductive de la bobine

d) l'inductance de la bobine

Solution

a) La valeur crête du flux est:

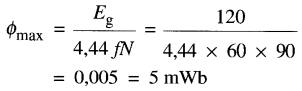
b) La valeur crête du courant magnétisant est:

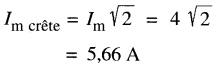
La FMM crête est:

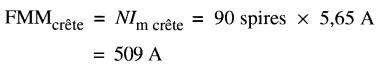
Notons que le flux atteint sa valeur crête Φ_max à l'instant où la FMM est de 509 A.

c) La réactance inductive de la bobine est :

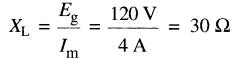
d) L'inductance de la bobine est :

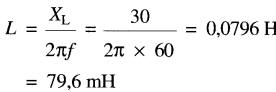
Transformateur élémentaire

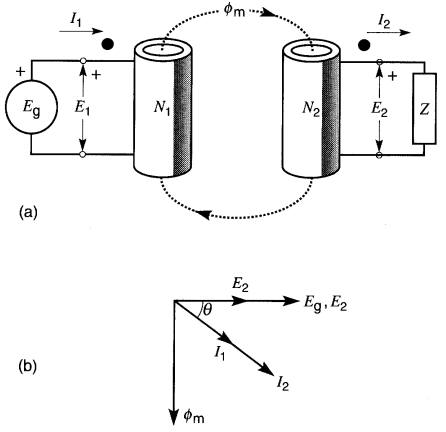
Sur la Fig. 30-4, une bobine à noyau d'air est alimentée par une source de tension E_g. Le courant magnétisant I_m produit un flux total Φ qui est dispersé autour de l'enroulement.

Figure 30-4 Définition du flux mutuel et du flux de fuite

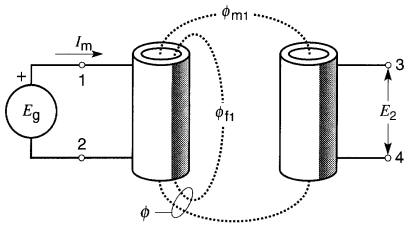
Si l'on approche de ce montage une deuxième bobine, une partie du flux Φ est captée (ou accrochée) par les spires de cette deuxième bobine et une faible tension E₂ est induite à ses bornes.

L'ensemble de ces deux bobines constitue un transformateur. La bobine raccordée à la source est appelée enroulement primaire (ou simplement «primaire») et l'autre est appelée enroulement secondaire (ou simplement «secondaire»).

Il existe une tension seulement entre les bornes 1.2 du primaire et les bornes 3.4 du secondaire.

Il n'existe aucune tension entre une des bornes du primaire et une des bornes du secondaire. Il s'ensuit que le secondaire est isolé électriquement du primaire.

Le flux Φ créé par le primaire peut être subdivisé en deux parties: un flux mutuel Φ_m1 qui accroche les spires du secondaire, et un flux de fuite Φ_f1, qui ne les accroche pas.

Lorsque les bobines sont éloignées l'une de l'autre, le flux mutuel est faible par rapport au flux total Φ; on dit alors que le couplage entre les bobines est faible.

On peut obtenir un meilleur couplage (et une tension E₂ plus grande) en rapprochant les deux enroulements.

Cependant, même si l'on colle le secondaire contre le primaire, le flux mutuel demeure faible par rapport au flux total Φ. Lorsque le couplage est faible, la tension E₂ est petite et, de plus, elle s'écrase dès qu'on applique une charge entre les bornes du secondaire.

Il faut donc trouver un moyen d'améliorer le couplage. On peut l'améliorer de beaucoup en bobinant le secondaire par-dessus le primaire.

Avec cette construction, la presque totalité du flux Φ créé par le primaire est accrochée par le secondaire. Le flux de fuite n'est plus qu'une petite fraction du flux total, ce qui augmente la valeur de la tension induite E₂ à vide et la maintient presque constante en charge.

Marques de polarité d'un transformateur

Dans la Fig. 30-4, les flux Φ_f1 , et Φ_m1 sont tous deux produits par le courant magnétisant I_m.

Par conséquent, les flux sont en phase, atteignant tous deux leur valeur crête en même temps. Ils passent aussi par zéro en même temps. Il s'ensuit que la tension E₂ atteint sa valeur crête en même temps que E_g.

Supposons qu'au moment où les tensions atteignent leur maximum, la borne 1 soit positive par rapport à la borne 2, et que la borne 3 soit positive par rapport à la borne 4 (Fig. 30-5).

Figure 30-5 Les bornes ayant la même polarité instantanée sont identifiées par un point noir

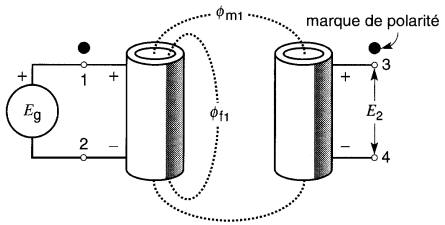
On dit alors que les bornes 1 et 3 possèdent la même polarité. On l'indique en plaçant un gros point noir vis-à-vis de la borne 1 et un autre vis-à-vis de la borne 3.

Ces points sont appelés marques de polarité.

On pourrait aussi bien placer les marques de polarité vis-à-vis des bornes 2 et 4, car elles deviennent à leur tour simultanément positives lorsque les tensions alternent. On peut donc placer les marques de polarité, soit à côté des bornes 1 et 3, soit à côté des bornes 2 et 4.

Propriétés des marques de polarité

Habituellement, un transformateur est logé dans un boîtier de sorte que seulement les bornes primaires et secondaires sont accessibles. Bien que les enroulements ne soient pas visibles, les règles suivantes s'appliquent quand on connait les marques de polarité.

1. Un courant qui entre par une marque de polarité produit une FMM dans le sens «positif». Par conséquent, il produit un flux dans le sens «positif» (Fig. 30-6).

Figure 30-6 Un courant qui entre par une borne portant une marque de polarité crée un flux dans le sens «positif»

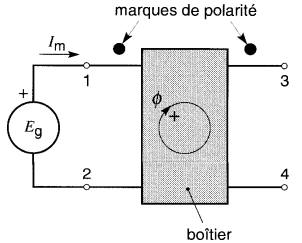
Inversement, un courant sortant d'une marque de polarité crée une FMM dans le sens «négatif».

Une FMM «négative» agit en sens inverse d'une FMM «positive».

2. Si une borne portant une marque de polarité est momentanément positive, toutes les bornes ayant une marque de polarité sont momentanément positives (par rapport à l'autre borne du même enroulement).

Ces règles nous permettent de tracer le diagramme vectoriel des circuits primaire et secondaire, même si ces deux enroulements sont électriquement isolés.

Par exemple, dans la Fig. 30-6, compte tenu des marques de polarité, la tension E₃₄ est nécessairement en phase avec la tension E₁₂.

LE TRANSFORMATEUR IDÉAL

Le transformateur idéal à vide; rapport de transformation

Avant d'entreprendre l'étude des transformateurs industriels, nous allons examiner les propriétés d'un transformateur idéal. Par définition, un transformateur idéal n'a aucune perte et son noyau est infiniment perméable.

De plus, le couplage entre le primaire et le secondaire est parfait. Par conséquent, un transformateur idéal n'a aucun flux de fuite. E

n pratique, les transformateurs ont des caractéristiques qui se rapprochent de celles d'un transformateur idéal. L'étude du transformateur idéal nous aidera donc à comprendre les propriétés des transformateurs réels.

La Fig. 30-7a montre un transformateur idéal dont le primaire et le secondaire possèdent respectivement N1 et N2 spires.

Figure 30-7 a. Transformateur idéal à vide. b. Diagramme vectoriel des grandeurs sinusoïdales

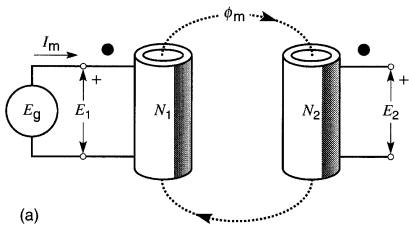
Le primaire est raccordé à une source E_g, et le secondaire est ouvert. Les tensions induites ont respectivement E₁ et E₂ volts.

Le flux Φ_max créé par le primaire est accroché complètement par le secondaire.

Comme sa valeur crête est Φ_max, on peut écrire les équations suivantes :

E₁ = E_g

E₁ = 4,44fN₁Φ_max

et

E₂ = 4,44fN₂Φ_max

En divisant la première équation par la deuxième, on tire l'expression du rapport de transformation d'un transformateur:

E₁ / E₂  = N₁ / N₂  (30-4)

où

E₁ = tension induite au primaire [V]

E₂ = tension induite au secondaire [V]

N₁ = nombre de spires du primaire

N₂ = nombre de spires du secondaire

Cette relation signifie que le rapport des tensions primaire et secondaire est égal au rapport des nombres de spires.

De plus, puisque les tensions primaire et secondaire sont produites par le même flux Φ_m, elles atteignent leurs valeurs maximales et minimales en même temps.

Le diagramme vectoriel pour la marche à vide est donné à la Fig. 30-7b.

Vu les marques de polarité du transformateur (points noirs), et les polarités des tensions (signes +), le vecteur E₂ est en phase avec le vecteur E₁.

Pour un transformateur dont le secondaire comporte moins de spires que le primaire, le vecteur E₂ est plus court que le vecteur E₁.

Comme pour toute inductance, le courant Im est déphasé de 90° en arrière de la tension E₁. Le vecteur représentant le flux Φ_m est en phase avec Im car le flux est créé par le courant magnétisant.

Cependant, comme il s'agit d'un transformateur idéal, le circuit magnétique est infiniment perméable, ce qui veut dire qu'un courant magnétisant infiniment petit suffit à créer le flux Φ_m.

Le diagramme vectoriel à vide est donc tel que le montre la Fig. 30-7b, mais I_m est infiniment petit.

Exemple 30-3

On applique une tension efficace de2400 V au primaire d'un transformateur abaisseur de tension, dont le primaire comporte 500 spires et le secondaire 25 spires.

a) Calculer la tension efficace induite au secondaire

b) Quelle est la valeur de la tension instantanée au secondaire au moment où la tension au primaire est de 37 V?

Solution

a) La tension induite dans chacune des spires de l'enroulement primaire est:

2400 V / 500 spires = 4,8 V/spire

Cette valeur est aussi celle de la tension induite dans chaque spire de l'enroulement secondaire.

La tension totale aux bornes du secondaire est donc :

E₂ = 4,8 V/spire x 25 spires = 120 V

On aurait pu calculer directement cette tension en utilisant le rapport de transformation.

De l'équation 30-4 on obtient:

E₂ = E₁ x N₂ / N₁ = 2400 x 25/500 = 120V

b) La tension au secondaire est 25/500 = 0,05 fois la tension au primaire à chaque instant.

Par conséquent, lorsque E₁ = 37 V, E₂ = 37 x 0,05 = 1,85 V.

Transformateur idéal en charge; rapport des courants

Raccordons une charge Z au secondaire d'un transformateur idéal (Fig. 30-8).

Figure 30-8

a. Transformateur idéal en charge ; il produit seulement un flux mutuel. b. Diagramme vectoriel des grandeurs sinusoïdales

Un courant I₂ circulera immédiatement.

Ce courant est donné par:

I₂  =  E₂  / Z

Noter que ce courant circule dans la charge ainsi que dans les N₂ spires du secondaire. La valeur de E₂ change-t-elle lorsqu'on branche la charge?

Avant de répondre à cette question, rappelons deux faits.

Premièrement, dans un transformateur idéal, le primaire et le secondaire sont couplés par le flux mutuel Φ_m seulement.

Par conséquent, le rapport de transformation en charge est le même qu'à vide, soit:

E₁ / E₂ = N₁ / N₂

Deuxièmement, comme la tension E_g de la source demeure constante, la tension E₁ (induite par Φ_m reste également constante.

Il s'ensuit que E₂ ne change pas lorsque la charge est branchée au secondaire.

Examinons maintenant les FMM qui sont engendrées par les enroulements primaire et secondaire. Tout d'abord, le courant I₂ produit une FMM secondaire N₂I₂.

Si elle agissait seule, cette FMM produirait un changement majeur dans le flux Φ_m.

Mais on vient de constater que le flux Φ_m ne change pas. Le flux Φ_m ne peut donc demeurer constant que si le primaire crée, à tout instant, une FMM N₁I₁ d'égale valeur mais opposée à N₂I₂.

Ainsi, le courant Ii circulant au primaire doit respecter la relation :

N₁I₁ =  N₂I₂    (30-5)

Afin de créer cette opposition instantanée, I₁ et I₂ doivent augmenter et diminuer en même temps. Il faut donc que I₁ et I₂ soient en phase.

De plus, pour que les FMM s'opposent, il faut que Il entre par la marque de polarité du primaire lorsque I₂ sort par la marque de polarité du secondaire (Fig. 30-8a).

Compte tenu de ce qui précède, on peut tracer le diagramme vectoriel du transformateur idéal en charge (Fig. 30-8b). Si l'on suppose une charge résistive-inductive, le courant I₂ sera en retard d'un angle θ sur la tension E₂.

Le flux Φ_m est toujours 90° en arrière de E_g, mais aucun courant magnétisant n'est requis, du fait qu'il s'agit d'un transformateur idéal dont le noyau a une perméabilité infinie.

Les courants I₁ et I₂ sont en phase et ils sont définis par l'équation:

I₁ / I₂ = N₁  / N₂     (30-6) 

où

I₁ = courant primaire [A]

I₂ = courant secondaire [A]

N₁ = nombre de spires au primaire

N₂ = nombre de spires au secondaire

En comparant les équations 30-4 et 30-6, on constate que le rapport des courants est l'inverse de celui des tensions. Autrement dit, ce que l'on gagne en tension, on le perd en courant et vice versa.

Des équations 30-4 et 30-6, on tire:

E₁I₁ =  E₂I₂    (30-7)

La puissance apparente absorbée au primaire est donc égale à la puissance apparente débitée par le secondaire. Il s'ensuit que les puissances active et réactive débitées par le secondaire sont exactement égales à celles absorbées par le primaire.

Conventions et représentation symbolique d'un transformateur idéal

Afin de se concentrer sur les propriétés fondamentales du transformateur idéal, il est utile de le représenter sous forme symbolique.

Ainsi, au lieu de tracer en détail les enroulements et le flux mutuel Φ_m, on montre un simple boîtier possédant les bornes primaires et secondaires (Fig. 30-9).

Figure 30-9a Symbole d'un transformateur idéal et diagramme vectoriel associé lorsque les tensions sont notées selon la méthode des polarités (+, -)

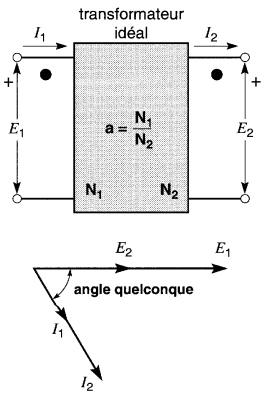
Les marques de polarité du transformateur (les deux points noirs) permettent d'indiquer la relation vectorielle entre les courants et les tensions au primaire et au secondaire. Pour les courants, nous adoptons les règles suivantes :

1. Le courant I₁ au primaire entre par la marque de polarité

2. Le courant I₂ au secondaire sort par la marque de polarité

Il s'ensuit que I₁ et I₂ sont en phase.

En ce qui concerne les tensions, deux notations sont possibles: l'une selon la méthode des polarités (+-), l'autre selon la méthodes des deux indices (voir Conventions de signes pour tensions et courants).

Lorsque les tensions sont indiquées selon la méthode des polarités, nous adoptons la règle suivante (Fig. 30.9a):

1. La tension primaire est indiquée par le symbole E₁ et sa polarité (+) est inscrite vis-à-vis de la marque de polarité du primaire

2. La tension secondaire est indiquée par le symbole E₂ et sa polarité (+) est inscrite vis-à-vis de la marque de polarité du secondaire

Cette règle assure que E₁ et E₂ sont en phase.

Lorsque les tensions sont indiquées selon la méthode des deux indices, nous adoptons la procédure suivante (Fig. 30-9b) :

Figure 30-9b Symbole d'un transformateur idéal et diagramme vectoriel associé lorsque les tensions sont notées selon la méthode des deux indices.

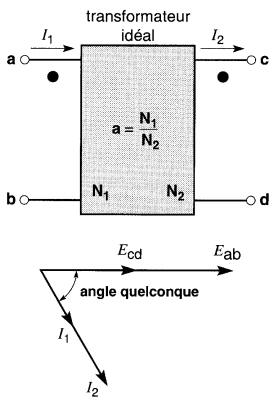
1. Les bornes sont identifiées par des symboles, tels que les lettres a, b, c, d.

2. En tenant compte des marques de polarité on peut immédiatement écrire les tensions primaire et secondaire qui sont en phase.

Ainsi, dans la Fig. 30-9b, E_ab et E_cd sont en phase, car les symboles a et c sont tous deux vis-à-vis d'un point noir.

Nous définissons aussi le rapport de transformation a, selon l'expression:

II s'ensuit que:

E₁ = a E₂ (Fig. 30-9a)

E_ab = a E_cd (Fig. 30-9b)

I₂ = a I₁ (Fig. 30-9a et 30-9b)

Exemple 30-4

Un transformateur idéal ayant 90 spires au primaire et 2250 spires au secondaire est branché sur une source de 200V, 60 HZ (Fig. 30-10a).

Figure 30-10 a. Voir exemple 30-4. b. Diagramme vectoriel des tensions et des courants

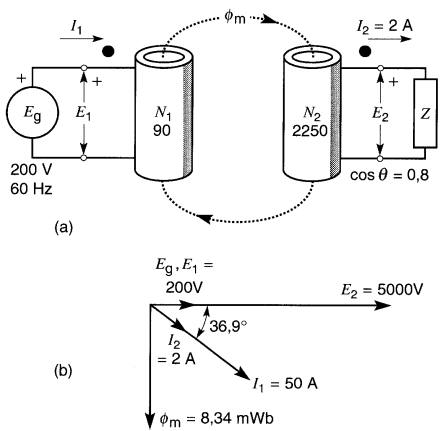
La charge tire un courant de 2A et son facteur de puissance est de 80 % en retard. Tracer le diagramme vectoriel.

Solution

En se référant à la Fig. 30-10a, la polarité des tensions E₁, E₂ et la direction des courants I₁ , I₂ sont indiquées conformément aux règles que nous venons de décrire.

Le rapport de transformation est :

a = N₁ / N₂ = 90 / 2250 = 0.04

La tension secondaire est donc :

E₂ = E₁ / a = 200 / 0.04 = 5000 V

Comme le facteur de puissance est 80 % en retard, il s'ensuit que I₂ est en retard sur E₂ d'un angle:

θ = arccos 0,8 = 36,9°

Le courant au primaire est :

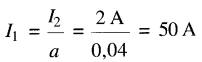
La valeur crête du flux est:

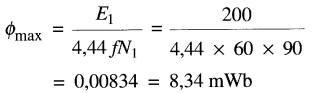
Le vecteur Φ_m est 90° en arrière de E_g et de E₁.

En prenant E_g comme vecteur de référence, on obtient le diagramme vectoriel montré à la Fig. 30-10b.

Rapport d'impédance

Le transformateur est utilisé pour modifier une tension ou un courant. Nous montrons ci-après que ces transformations de la tension et du courant produisent aussi une transformation d'impédance.

Considérons, par exemple, la Fig. 30-11, où un transformateur idéal est branché entre une source E_g et une charge ayant une impédance Z_s.

Figure 30-11

a. Un transformateur idéal peut transformer la valeur d'une impédance.

b. l'impédance vue par la source est a² fois l'impédance réelle.

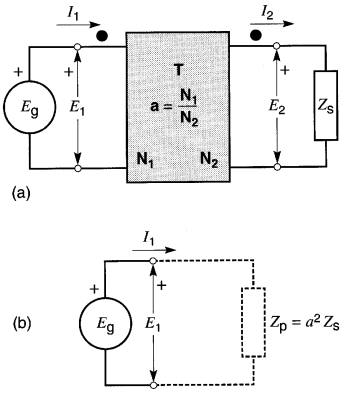
Le rapport de transformation étant a, on peut écrire:

E1 = aE2 et I1 = I2 / a

Les bornes secondaires «voient» une impédance Z_s  donnée par:

E2 / I2 = Z_s     (30-9)

D'autre part, la source E_g «voit» une impédance Z_p donnée par:

 Z_p =  E1 / I1   (30-10)

En substituant les équations 30-8 et 30-9 dans l'expression 30-10, on obtient:

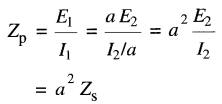
Par conséquent, on peut écrire:

Z_p = a² Z_s      (30-11) 

où

Z_p = impédance vue entre les bornes du primaire [Ω]

Z_s = impédance réelle entre les bornes du secondaire [Ω]

a = rapport de transformation

Cette expression révèle que l'impédance Zp vue par la source est a² fois l'impédance réelle (Fig. 30-11b).

Un transformateur idéal a donc la propriété remarquable de pouvoir augmenter ou abaisser la valeur d'une impédance, quelle que soit sa nature.

Cette transformation est bel et bien réelle. Un transformateur permet de changer la valeur de n'importe quelle composante, que ce soit une résistance, un condensateur ou une inductance.

Par exemple, si l'on branche une résistance de 100Ω au secondaire d'un transformateur ayant un rapport de transformation a = 0,2, elle apparaît au primaire comme une résistance de

Rp = 100 x (0,2)² = 4 Ω

De même, un condensateur possédant une réactance capacitive X_c = 100 Ω apparaîtra au primaire comme un condensateur ayant une réactance de 4 Ω.

Comme la réactance est inversement proportionnelle à la capacitance, il s'ensuit que la capacitance vue par la source est 25 fois plus grande que la capacitance réelle.

On peut donc augmenter (ou diminuer) la capacitance d' un condensateur ou l'inductance d'une bobine à l'aide d'un transformateur.

Déplacement des impédances du secondaire au primaire et vice versa

Pour résoudre un circuit comprenant un transformateur, il est parfois utile de l'éliminer afin de simplifier le circuit. Cela peut se réaliser en transférant les impédances du côté secondaire au côté primaire.

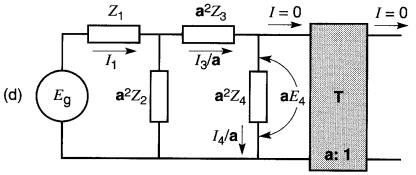
Considérons le circuit de la Fig. 30-12a composé de quatre impédances et d'un transformateur alimentés par une source E_g.

Figure 30-12

a. Montage composé de 4 impédances et d'un transformateur idéal

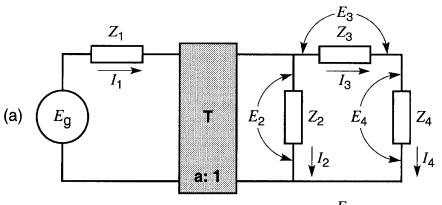
b. L'impédance Z2 est rapportée au côté primaire

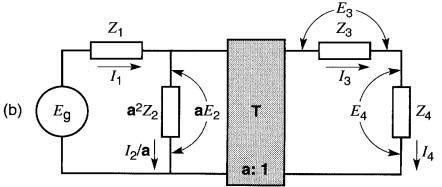
c. Z2 et Z3 sont rapportées au côté primaire 

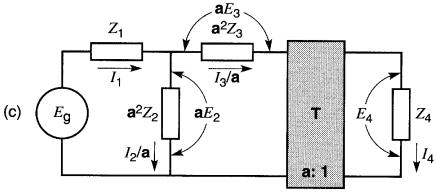
d. Toutes les impédances sont rapportées au côté primaire. Le transformateur ne porte plus aucune charge.

e. Circuit équivalent après élimination du transformateur.

Le transformateur a un rapport de transformation a.

On peut progressivement déplacer au primaire les impédances situées du côté secondaire, comme l'indiquent les Fig. 30-12b à 30-12e.

On constate que l'arrangement série-parallèle des éléments demeure intact, mais la valeur des impédances ainsi transférées est multipliée par le facteur a².

En même temps, la tension réelle aux bornes de chaque élément est multiplie par a et le courant qu'il porte est divisé par a. Comparer, par exemple, la tension et le courant dans l'élément Z₂ avant et après le transfert (Fig. 30-12a et 30-12b).

Si l'on transfère toutes les impédances, le transformateur se retrouve à l'extrême droite du circuit (Fig. 30-12d). On constate que le secondaire est alors ouvert, ce qui implique que les courants au primaire et au secondaire sont nuls.

On peut donc éliminer le transformateur sans que le circuit soit affecté (voir Fig. 30-12e). Dans cette figure, les impédances sont toutes ramenées du côté primaire du transformateur.

Comme le transformateur a disparu, le circuit peut être résolu par les méthodes habituelles. En général, lorsqu'on transfère une impédance, la tension réelle à ses bornes est multipliée par le rapport de transformation.

Si l'impédance est transférée du côté où la tension est plus élevée, la tension aux bornes de l'impédance ainsi transférée augmente dans les mêmes proportions.

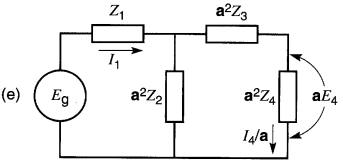
Il est parfois utile de transférer les éléments primaires au côté secondaire (Fig. 30-13a).

Figure 30-13 Transfert progressif des éléments du côté primaire au côté secondaire

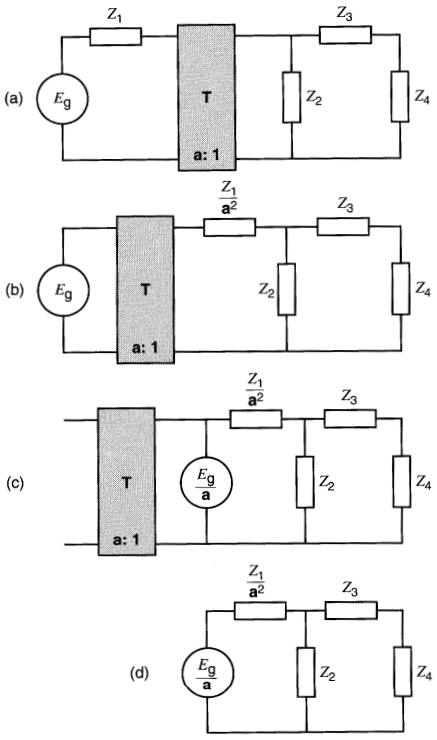
On procède alors de la même manière mais la valeur des impédances ainsi transférées est divisée par a2 (Fig. 30-13b).

On peut même transférer la source au côté secondaire; sa tension devient alors E_g/a.

On constate de nouveau que les courants dans le transformateur (situé maintenant à l'extrême gauche, Fig. 30-13c) sont nuls, ce qui permet de l'éliminer, pour arriver au montage de la Fig. 30-13d.

Exemple 30-5

Soit le montage de la Fig. 30-14 dans lequel le transformateur idéal a un rapport de transformation a = N1 / N2 = 2

Figure 30-14 Voir exemple 30-5

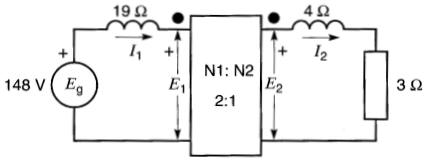
a) Tracer le circuit équivalent en rapportant toutes les impédances au côté primaire. Calculer la valeur de I1.

b) Tracer le circuit équivalent en rapportant toutes les impédances au côté secondaire. Calculer la valeur de I2.

Solution

a) Lorsque les impédances de 4 Ω et 3 Ω sont rapportées au primaire, leurs valeurs sont augmentées dans le rapport (N1 / N2)², soit par un facteur 2² = 4 .

Cela donne le circuit équivalent de la Fig . 30-15.

Figure 30-15 Les impédances sont rapportées au côté primaire

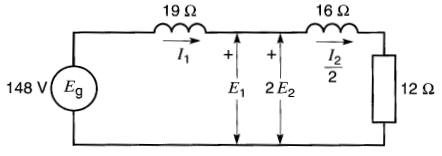
L'impédance de ce circuit est:

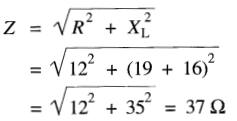    éq. 24-3

Il s'ensuit que:

I1 = E_g / Z = 148V / 37Ω = 4A

De plus, puisque I1 = I2 / 2, il s'ensuit que I2 = 8 A.

b) Lorsque les éléments sont tous rapportés au côté secondaire, l'impédance de 19Ω devient :

X_L = 19 / a² = 19 / 4 = 4,75 Ω

La tension de 148 V devient :

E'_g = 148 V / a = 148 V / 2 = 74 V

Ce qui donne le circuit équivalent de la Fig. 30-16.

Figure 30-16 Les impédances sont rapportées au côté secondaire

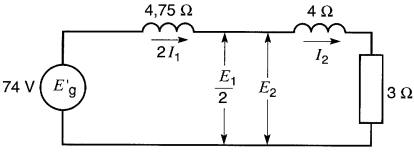
L'impédance du circuit est:

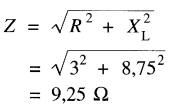
II s'ensuit que:

I2 = E'_g / Z = 74V / 9,25Ω

Le diagramme vectoriel du montage réel est donné à la Fig. 30-17.

Figure 30-17 Diagramme vectoriel du circuit de la Fig. 30-14

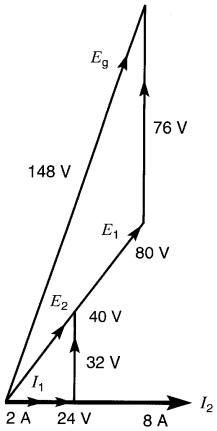
On a pris le courant I2 comme vecteur de référence. Le lecteur vérifiera que les tensions aux bornes des réactances et de la résistance sont respectivement de 76 V, 32 V et 24 V, telles qu'indiquées.

TRANSFORMATEURS UTILISÉS EN PRATIQUE

Nous venons d'étudier les propriétés du transformateur idéal. Cependant, en pratique, les transformateurs réels ne sont pas parfaits et notre analyse doit en tenir compte.

Ainsi, les enroulements d'un transformateur réel possèdent une résistance, et le noyau n'est pas infiniment perméable. De plus, le flux créé par le primaire n'est pas complètement accroché par le secondaire, de sorte qu'il faut tenir compte des flux de fuite.

Enfin, les pertes dans le fer contribuent à l'échauffement du transformateur et diminuent son rendement. Nous verrons que l'on peut représenter un transformateur réel par un circuit équivalent composé d'un transformateur idéal, de résistances et de réactances.

Ce circuit nous permettra de décrire toutes les propriétés d'un transformateur, même lorsqu'il est branché en parallèle avec d'autres transformateurs.

Enfin, pour mieux saisir l'ordre de grandeur des éléments composant le circuit équivalent du transformateur, nous aurons recours aux valeurs relatives, soit le système p.u. 30.11

Transformateur idéal comportant un noyau réel

Le noyau d'un transformateur idéal est parfaitement perméable et ne présente aucune perte. Qu'arrive-t-il si on le remplace par un autre ayant des pertes par hystérésis et par courants de Foucault et dont la perméabilité n'est pas infinie?

Ces imperfections peuvent être représentées au moyen d'une résistance R_m et d'une réactance X_m branchées en parallèle avec le primaire d'un transformateur idéal (Fig . 30-18a).

Figure 30-18 a. Circuit d'un transformateur idéal comportant un noyau réel. b. Diagramme vectoriel des variables

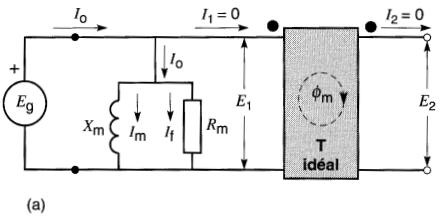
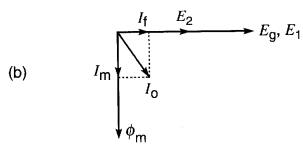
La résistance R_m représente les pertes dans le fer et la chaleur qu'elles dégagent. Un faible courant I_f est tiré de la ligne pour fournir ces pertes. La réactance magnétisante X_m est un indice de la perméabilité du noyau.

Ainsi, à une faible perméabilité, correspond une valeur de X_m relativement basse.

Le courant I_m est le courant magnétisant requis pour créer le flux dans le noyau. Les valeurs de R_m et X_m sont données par les équations suivantes:

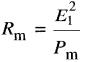    (30-12)

    (30-13)

où

R_m = résistance représentant les pertes dans le fer  [Ω]

X_m = réactance magnétisante du primaire [Ω]

E1 = tension induite au primaire [V]

P_m = pertes dans le fer [W]

Q_m = puissance réactive requise pour créer le flux mutuel θ_m [var]

Pour créer le flux dans un noyau imparfait, on a besoin d'un courant I_o égal à la somme vectorielle de I_f et de I_m.

Ce courant s'appelle courant d'excitation. La Fig. 30-18b montre le diagramme vectoriel de ce transformateur imparfait lorsqu'il fonctionne à vide.

Le flux mutuel est encore donné par l'équation 30-3 :

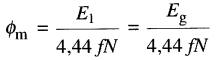
Exemple 30-6

Un transformateur de 20 kVA, 120 V/600 V, fonctionnant à vide, tire un courant de 5 A lorsqu'il est raccordé à une source de 120 V, 60 Hz (Fig . 30-19a).

Figure 30-19 Voir exemple 30-6

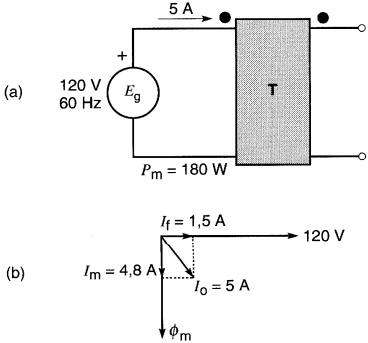
Un wattmètre indique une puissance de 180 W.

Calculer :

a) la puissance réactive absorbée par le noyau

b) la valeur de R_m et de X_m

c) les valeurs de I_f, I_m et I_o.

Solution

a) La puissance apparente fournie au noyau est:

S_m = E_gI_o = 120 V x 5 A = 600 VA

Les pertes dans le fer sont:

P_m = 180 W

La puissance réactive absorbée par le noyau est :

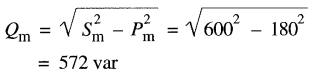
b) L'impédance correspondant aux pertes dans le fer est:

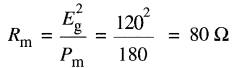
La réactance magnétisante est :

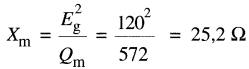
c) Le courant requis pour fournir les pertes dans le fer est:

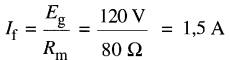
Le courant magnétisant est:

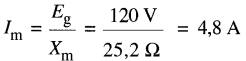
On vérifie que le courant d'excitation est:

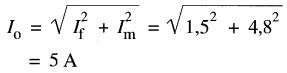
Le diagramme vectoriel est montré à la Fig . 30-19b.

Transformateur idéal à couplage partiel

Nous venons d'étudier le comportement d'un transformateur idéal lorsque son noyau est imparfait.

Supposons maintenant que le noyau soit idéal, mais que le couplage entre le primaire et le secondaire soit imparfait.

Le nombre de spires au primaire et au secondaire est respectivement N₁ et N₂ et on suppose que la résistance des enroulements est nulle. Considérons alors un tel transformateur raccordé à une source E_g et fonctionnant à vide (Fig. 30-20).

Figure 30-20 Transformateur idéal comportant un noyau parfait et un couplage relativement faible

 Puisque le noyau est parfait, le courant I₁ au primaire est nul.

Branchons alors une charge Z au secondaire tout en maintenant la tension E_g fixe (Fig. 30-21).

Figure 30-21 Flux mutuels et flux de fuite lorsque le transformateur est sous charge. Les flux de fuite sont d'autant plus grands que le couplage est faible. Noter que le flux θ_m1 n'a pas la même valeur que dans la Fig. 30-20.

Cette manoeuvre simple entraîne une série d'événements que nous énumérons ci-après:

1 . Des courants I₁ et I₂ commencent à circuler dans les enroulements primaire et secondaire.

Ils sont reliés par l'équation 30-6 :

I₁ / I₂ = N₂ / N₁

2. I₂ produit une FMM N₂I₂ et I, produit une FMM N₁I₁. Ces FMM agissent en sens contraires car lorsque I, entre par la marque de polarité 1, I₂ sort par la marque de polarité 3.

3 . La FMM N₁I₁ produit un flux total θ₁. Comme le couplage est imparfait, seulement une partie θ_m1 de ce flux est accrochée par le secondaire, alors que l'autre partie θ_f1, ne l'est pas. Le flux θ_f1, s'appelle flux de fuite du primaire.

4. La FMM N₂I₂ produit un flux total θ₂. Une partie θ_m2 de ce flux est accrochée par le primaire, alors que l'autre portion θ_f2 ne l'est pas. Le flux θ_f2 s' appelle flux de fuite du secondaire.

On constate donc qu'en raison des flux de fuite, les FMM créées par I₁ et I₂ changent complètement la configuration du champ magnétique par rapport au cas sans charge.

Comment analyser cette nouvelle situation?

En se référant à la Fig. 30-21, nous établissons les cinq points suivants :

1 . Étant donné que les flux mutuels θ_m1 et θ_m2 suivent le même chemin dans le noyau, on peut les combiner en un seul flux mutuel om (Fig. 30-22). Ce flux est créé par l'action conjointe des FMM du primaire et du secondaire.

Figure 30-22 Le flux mutuel est produit par l'action combinée des FMM N₁I₁ et N₂I₂

2. Le flux de fuite of, est créé par la FMM N₁I₁; par conséquent θ_f1 est en phase avec Il. Par un raisonnement analogue on trouve que θ_f2 est en phase avec I₂.

3. La tension E_S induite entre les bornes du secondaire est composée de deux tensions :

(i) une tension E₂ due au flux mutuel θ_m, donnée par:

E₂ = 4,44 fN₂θ_m

(ii) une tension E_f2 due au flux de fuite θ_f2, donnée par:

E_f2 = 4,44 fN₂θ_f2

4. De la même façon, la tension E_p induite aux bornes du primaire est composée de deux tensions:

(iii) une tension E₁ due au flux mutuel θ_m, donnée par:

El = 4,44 fN₁θ_m

(iv) une tension E_f1 due au flux de fuite θ_f1 donnée par:

E_f1 = 4,44 fN₁θ_f1

5. Enfin, la tension E_p induite au primaire est égale à la tension E_g de la source.

À l'aide de ces données, nous sommes en mesure de développer le circuit équivalent du transformateur.

Réactances de fuite au primaire et au secondaire

Il est plus facile d'identifier les quatre tensions E₁, E₂, E_f1, et E_f2 en réarrangeant le circuit du transformateur comme l'indique la Fig. 30-23.

Figure 30-23 Ce circuit est électriquement identique à celui de la Fig . 30-22

Afin de mettre en évidence les deux flux Φm et Φf2 accrochés par l'enroulement N₂, l'enroulement secondaire est représenté deux fois.

La tension E_f2 apparaît comme une chute de tension aux bornes d'une réactance. Cette réactance s'appelle réactance de fuite du secondaire, et sa valeur est donnée par:

De même, l'enroulement primaire est représenté deux fois.

La tension E_f1, apparaît alors comme une chute de tension à travers la réactance de fuite du primaire.

Sa valeur est donnée par:

Les réactances de fuite sont montrées de façon conventionnelle à la Fig. 30-24.

Figure 30-24 Réactances de fuite et résistances des enroulements primaire et secondaire

On y a ajouté les résistances R₁ et R₂ des enroulements primaire et secondaire, les.quelles sont évidemment en série avec leurs enroulements respectifs.

Circuit équivalent d'un transformateur

En examinant la Fig. 30-24, on constate que le transformateur situé à l'intérieur du rectangle pointillé ne possède plus aucune perte ni flux de fuite. C'est donc un transformateur idéal possédant toutes les propriétés décrites dans les sections précédentes.

 Par exemple, on peut rapporter les impédances du côté secondaire au côté primaire en multipliant leurs valeurs par (N₁/N₂)².

Si l'on ajoute les éléments R_m et X_m pour représenter un noyau réel avec pertes, on obtient le circuit équivalent complet d'un transformateur industriel (Fig . 30-25).

Figure 30-25 Circuit équivalent d'un transformateur réel. Le rectangle T représente un transformateur idéal

Dans ce circuit, seules les bornes primaires 1, 2 et les bornes secondaires 3, 4 sont accessibles.

Les autres composants, y compris le transformateur idéal T, demeurent cachés à l'intérieur du transformateur. Cependant, il est possible de déterminer la valeur de ces composants au moyen de tests appropriés.

Exemple 30-7

On donne l'information suivante relativement aux Fig.30-22 et 30-23:

N₂ = 180 spires    Φm = 20 mWb (crête)

18 A, 60 Hz    Φ_f2 = 0,3 mWb (crête)

Calculer:

a) la valeur de E₂ induite par le flux mutuel Φm

b) la valeur de E_f2 induite par le flux de fuite Φ_f2

c) la valeur de la réactance de fuite X_1-2

Solution

a) La valeur de E₂ est:

E₂ = 4,44fN₂Φm = 4,44 x 60 x 180 x 0,02 = 959 V

b) La valeur de E_f2 est:

E_f2 = 4,44fN₂Φ_f2 = 4,44 x 60 x 180 x 0,0003 = 14,39 V

c) La réactance de fuite du secondaire est :

X_f2 = E_f2 / I₂ = 14,39 V / 18 A = 0,8Ω

Simplification du circuit équivalent

Le circuit équivalent du transformateur présenté à la Fig. 30-25 est très général, de sorte qu'il peut représenter le comportement du transformateur pour toutes les conditions de charge.

En pratique, selon que le transformateur fonctionne à vide ou en charge, on peut négliger certains éléments, ce qui simplifie énormément les calculs. Nous examinons ces deux cas ci-après.

1. Transformateur fonctionnant à vide.

Lorsque le transformateur fonctionne à vide (Fig . 30-26), la charge est nulle et le courant I₂ = 0; il s'ensuit que I₁ = 0 car T est un transformateur idéal.

Figure 30-26 Circuit équivalent complet lorsque le transformateur fonctionne à vide

Par conséquent, seul le courant d'excitation I_o circule dans R₁ et X_f1.

Comme l'impédance de ces deux éléments est faible et que I_o est petit, la chute de tension correspondante est négligeable, de sorte que la pleine tension E_p apparaît aux bornes de la branche d'excitation. Le circuit à vide prend donc la forme simple montrée à la Fig. 30-27. La tension E_p aux bornes du transformateur est évidemment égale à la tension E_g de la source.

Figure 30-27 Circuit équivalent simplifié lorsque le transformateur fonctionne à vide

2. Transformateur fonctionnant en charge.

Lorsque la charge d'un transformateur est plus grande que 20 % de sa puissance nominale, la valeur de I_o est négligeable devant celle de I₁ (Fig. 30-28).

Figure 30-28 Circuit équivalent complet lorsque le transformateur est en charge

On peut donc négliger la branche d'excitation, ce qui donne le circuit de la Fig. 30-29.

Figure 30-29 Circuit équivalent simplifié lorsque la charge est supérieure à 20 % de la puissance nominale du transformateur

Le circuit se simplifie encore davantage lorsque toutes les impédances sont rapportées au côté primaire. Ce transfert d'impédances permet d'éliminer le transformateur idéal T (Fig. 30-30), selon la technique expliquée à la section plus-haut.

Figure 30-30 Circuit équivalent lorsque les impédances sont rapportées au côté primaire

Enfin, en regroupant les résistances et les réactances primaires et secondaires, on obtient le circuit de la Fig . 30-31.

Figure 30-31 Résistance totale R_p , réactance de fuite totale X_p et impédance totale Z_p du transformateur rapportées au primaire

Dans ce circuit:

R_p = R₁ +a²R₂     (30-14)

X_p = X_n + a²X_f2     (30-15)

ou

R_p = résistance totale du transformateur rapportée au primaire [Ω]

X_p = réactance totale du transformateur rapportée au primaire [Ω]

L'ensemble R_p et X_p constitue l'impédance totale Z_p du transformateur rapportée au primaire.

L'équation 24-3 permet d'écrire:

Lorsque la puissance nominale du transformateur dépasse 500 kVA, le calcul des tensions et courants est simplifié encore davantage.

En effet, dans ce cas, la valeur de X_p est au moins 5 fois plus grande que R_p, de sorte que R_p devient négligeable. Cependant, pour les calculs de pertes et d'échauffement, R_p doit évidemment être prise en considération.

Le circuit équivalent relativement complexe de la Fig. 30-25 se résume donc à une simple réactance X_p reliant la source et la charge (Fig. 30-32).

Figure 30-32 L'impédance totale d'un gros transformateur est pratiquement égale à sa réactance de fuite

Construction du transformateur

Habituellement, la conception des transformateurs utilisés en pratique est telle que leurs propriétés se rapprochent de celles du transformateur idéal.

Ainsi, afin d'obtenir une bonne perméabilité, le noyau est fait en acier de bonne qualité. De plus, pour minimiser les pertes dans le fer, le noyau est laminé en utilisant de l'acier au silicium.

Il s'ensuit que le courant magnétisant I_m, est au moins 5000 fois plus petit que si le noyau était composé d'un matériau non magnétique. Le courant I_f fournissant les pertes dans le noyau est de 2 à 10 fois plus faible que le courant magnétisant I_m.

On réussit à diminuer les réactances de fuite X_f1 et X_n en bobinant le primaire et le secondaire l'un par-dessus l'autre, tout en réduisant la distance qui les sépare.

Cependant, afin de conserver une isolation adéquate entre les enroulements, on ne peut diminuer cette distance en deçà d'une valeur critique. Autrement, l'isolation risque de claquer lors des surtensions dues aux chocs de foudre ou aux manoeuvres sur le réseau.

Le couplage étant excellent, il s'ensuit que la tension secondaire reste très proche de N₂IN₁ fois la tension primaire. Cela assure une bonne régulation de la tension en fonction de la charge.

De plus, afin d'assurer un bon rendement, on cherche à limiter les pertes Joule en minimisant les résistances R₁ et R₂.

La Fig. 30-33 montre un transformateur dont le primaire et le secondaire sont divisés en deux sections. chacune d'elles étant bobinée sur une des jambes du noyau.

Figure 30-33

a. Construction d'un transformateur montrant le noyau et la façon dont les enroulements primaire et secondaire sont montés

b. Circuit montrant comment les deux sections de chaque enroulement sont raccordées

Le primaire (bornes H₁, H₂) est enroulé pardessus le secondaire (bornes X₁, X₂).

Le nombre de spires des enroulements primaire et secondaire est proportionnel à la tension (éq. 30-1). D'autre part, le courant nominal dans un enroulement est inversement proportionnel à la tension . Il s'ensuit que la quantité de cuivre (ou d'aluminium) requise pour les enroulements respectifs est à peu près la même.

En pratique, la bobine extérieure (le primaire) pèse un peu plus car la longueur moyenne des spires est plus grande.

 Mentionnons qu'en pratique le transformateur est parfaitement réversible en ce sens que le primaire peut agir comme secondaire, et vice versa.

Marques de polarité d'un transformateur de puissance

Jusqu'à présent nous avons indiqué la polarité des bornes d'un transformateur par deux points noirs au primaire et au secondaire. Ce type d'identification est utilisé surtout pour les transformateurs servant à l'instrumentation.

Cependant, pour les transformateurs de puissance, les bornes sont désignées par les symboles H₁ et H2 pour l'enroulement à haute tension, et par X₁ et X₂ pour l'enroulement à basse tension.

Par convention, lorsque H₁ est instantanément (+) par rapport à H₂, X₁ est (+) par rapport à X₂. On dit alors que H₁ et X₁ ont la même polarité.

En fait, H₁ et X₁ remplacent les deux points noirs. Bien que les marques de polarité d'un transformateur soient connues lorsque les symboles H₁, H₂, X₁ et X₂ sont donnés, il est d'usage de disposer les quatre bornes d'une façon conventionnelle selon que la polarité du transformateur est additive ou soustractive.

On dit qu'un transformateur a une polarité additive lorsque la borne haute tension H₁, montée sur la cuve du transformateur, est diamétralement opposée à la borne basse tension X₁. La polarité est dite soustractive lorsque la borne H₁ est physiquement en regard de la borne X₁ (Fig . 30-36).

Figure 30-36 La polarité additive et soustractive d'un transformateur dépend de l'orientation de ses bornes

Si l'on sait qu'un transformateur a une polarité additive ou soustractive, il n'est donc pas nécessaire d'identifier les bornes par des symboles H₁, H₂, X₁, X₂.

L'origine de ces dénominations de polarité additive et soustractive sera expliquée à la section suivante.

Les normes veulent que la polarité soit soustractive pour tout transformateur ayant une capacité supérieure à 200 kVA, pour autant que la tension primaire dépasse 8660 V.

Dans le cas contraire, la polarité est additive.

Test de polarité

La polarité d'un transformateur peut être déterminée facilement à l'aide du test suivant (Fig . 30-37):

Figure 30-37 Détermination de la polarité d'un transformateur avec une source à courant alternatif

1 . Connecter un cavalier J entre une borne de l'enroulement haute tension (HT) et la borne adjacente de l'enroulement basse tension (BT)

2. Brancher un voltmètre E_X entre les deux autres bornes

3 . Brancher un deuxième voltmètre E_p aux bornes de l'enroulement HT

4. Brancher l'enroulement haute tension à une source à courant alternatif, E_g. Lors de l'essai, on peut utiliser une tension E_g de l'ordre de 120 V, 60 Hz, même si la tension nominale HT est de plusieurs centaines de kilovolts.

Si la lecture E_X est supérieure à celle de E_p, la polarité est additive.

Par conséquent, les bornes H₁ et X₁ sont diamétralement opposées. Dans le cas contraire, la polarité est soustractive, et les bornes H₁ et X₁ sont adjacentes.

Dans ce test de polarité, le cavalier (composé d'un simple fil) sert à connecter la tension secondaire E_s en série avec la tension primaire E_p.

Par conséquent, suivant la polarité, on obtient l'une des deux possibilités suivantes:

E_X =E_p + E_S ou E_X = E_p .E_S

d'où l'origine des expressions «polarité additive» et «polarité soustractive» .

Exemple 30-8

Au cours d'un essai de polarité sur un transformateur de 500 kVA. 69 kV/600 V (Fig. 30-37), on a obtenu les lectures suivantes:

 E_p = 118V

E_X = 117V

Déterminer la polarité du transformateur et identifier les marques de polarité H₁, X₁.

Solution

La polarité est soustractive car E_X est inférieure à E_p.

Par conséquent, les bornes reliées par le cavalier doivent porter les symboles H₁ et X₁ (ou H₂ et X₂).

La Fig. 30-38 illustre un autre montage qui peut servir pour déterminer les marques de polarité d'un transformateur.

Figure 30-38 Détermination des marques de polarité avec une source à courant continu

Une pile sèche est raccordée aux bornes à basse tension du transformateur à travers un interrupteur, et un voltmètre à c.c. est branché aux bornes à haute tension.

Lors de la fermeture de l'interrupteur, une tension est induite dans l'enroulement à haute tension.

Si à cet instant l'aiguille du voltmètre dévie dans le bon sens, la borne du transformateur reliée à la borne positive (+) du voltmètre est marquée H₁ et l'autre est marquée H₂.

Quant aux bornes à basse tension, celle qui est reliée au pôle positif (+) de la pile est marquée X₁ et l'autre est marquée X₂.

Réglage de la tension; transformateur à rapport variable

cause des chutes de tension dans les lignes de distribution, la tension sur une partie du réseau est parfois constamment inférieure à la tension nominale. Par exemple, un transformateur ayant un rapport de transformation de 2400 à 120 V peut être branché sur une ligne de distribution dont la tension n'est que de 2000 V au lieu de 2400 V.

Dans ces conditions, la tension recueillie au secondaire n'est plus que de 100 V.

Si la charge est constituée de lampes à incandescence, il en résulte une diminution de l'intensité d'éclairage ; si la charge est formée d'éléments chauffants, la puissance dissipée dans ces appareils est fortement réduite.

Enfin, si la charge est composée de moteurs, leur démarrage peut être long et difficile. Pour remédier à ces inconvénients, on dispose des prises de réglage sur l'enroulement primaire des transformateurs.

Par exemple, dans le cas de la Fig. 30-39, ces prises permettent de modifier le rapport de transformation de façon à changer la tension secondaire de 4 1/2 %, 9 % ou 13 1/2 %.

Figure 30-39 Prises au primaire d'un transformateur et tableau donnant le réglage de la tension

Elles permettent donc de garder la tension secondaire à sa valeur nominale même si la tension appliquée au primaire est de 4 1/2 %, 9 % ou 13 1/2 % plus faible que la tension nominale.

Ainsi, pour le transformateur représenté à la Fig. 30-39, si la tension de ligne n'est que de 2076 V (13,5 % inférieure à la tension nominale de 2400 V) on peut utiliser la prise 5, c'est-à-dire les bornes 1 et 5 pour maintenir la tension secondaire à 120 V.

Certains transformateurs sont conçus pour changer de prise automatiquement lorsque la tension secondaire s'écarte d'une valeur préétablie. Ces transformateurs régulateurs de tension peuvent maintenir la tension à ± 2 % quelles que soient les fluctuations de la tension primaire survenant durant la journée.

Courbe de saturation et tension d'utilisation

Supposons que l'on augmente graduellement la tension E_p au primaire d'un transformateur, le secondaire étant ouvert. Le flux mutuel Φ_m, augmente proportionnellement à la tension, conformément à l'équation 30-3.

Par conséquent, le courant d'excitation I_o augmente graduellement. Cependant, dès que l'acier commence à se saturer, la composante I_n, doit augmenter brusquement afin de créer le flux requis .

La Fig. 30-40 montre la courbe de saturation E vs I_o d'un transformateur de 500 kVA, 15 kV/600 V, prise du côté de l'enroulement à haute tension.

Figure 30-40 Courbe de saturation d'un transformateur de 500 kVA, 15 kV/600 V, 60 Hz. Le courant d'excitation Io augmente brusquement dès que l'on dépasse la tension nominale de 15 kV

Tant que le flux mutuel est inférieur au coude de la courbe de saturation Φ-I de l'acier, le courant d'excitation reste faible et sensiblement proportionnel à la tension.

Mais au-delà ce coude, le courant augmente brusquement. Cette condition anormale de fonctionnement provoque une augmentation modérée des pertes dans le fer, mais entraîne une très forte augmentation du courant d'excitation.

On observe sur la Fig. 30-40 que le courant d'excitation est de 0,5 A alors que le courant de pleine charge est de 33 A. C'est dire qu'en régime normal, I_o représente seulement 0,5/33 = 1,5 % du courant nominal.

La densité de flux crête dans les transformateurs est généralement comprise entre 1,5 T et 1,7 T, ce qui correspond approximativement au coude de la courbe de saturation.

On peut appliquer sans problème une tension de 10 % supérieure à la tension nominale, mais si l'on doublait cette tension, le courant d'excitation excéderait le courant de pleine charge de l'enroulement.

La relation non linéaire entre la tension et le courant d'excitation révèle que les impédances R_m et X_m (Fig. 30-25) ne sont pas aussi constantes qu'on pourrait le croire. Alors que R_m demeure assez constante, X_m diminue rapidement lorsqu'on dépasse la densité de flux normale.

Toutefois, en régime normal, les transformateurs fonctionnent près de leur tension nominale, si bien que l'on peut considérer que R_m et X_m demeurent pratiquement constantes, même lorsque la charge varie.

La non-linéarité de la courbe de saturation provoque une distorsion du courant d'excitation, même lorsque le flux est sinusoïdal . Lorsqu'on connaît la forme de la courbe d' hystérésis donnant la relation flux/courant du noyau (Fig. 30-40b), on peut déduire la forme d'onde du courant d'excitation. La marche à suivre est expliquée dans l'exemple encadré.

On verra lors d'une étude des harmoniques (section Commande industrielle des moteurs) que ce courant non sinusoïdal comprend une composante fondamentale sinusoïdale à 60 Hz plus des composantes sinusoïdales à des fréquences multiples de 60 Hz (harmoniques).

La composante fondamentale du courant contient une composante qui est en phase avec la tension. C'est cette composante du courant qui fournit les pertes dans le fer.

Forme d'onde du courant d'excitation

Un transformateur de 30 kVA, 120 V/24 V, 60 Hz possède un primaire de 45 spires. Lorsqu'il est alimenté par une source sinusoïdale de 120 V, il tire un courant d'excitation I_o de 7,32 A efficace.

En appliquant la formule (30-1), on trouve que le flux atteint une valeur crête de 10 mWb (Fig. 30-40a).

Figure 30-40b Courbe d'hystérésis d'un transformateur

La courbe d'hystérésis du noyau montre les valeurs instantanées du flux 0en fonction du courant d'excitation Io (Fig. 30-40b).

Figure 30-40b Courbe d'hystérésis d'un transformateur

Donc, pour chaque valeur de 0 dans la Fig. 30-40a il existe, selon la Fig. 30-40 b, une valeur correspondante de Io. Le tableau ci-dessous donne les valeurs du flux et du courant Io au cours d'un cycle de 360° . Il nous permet de tracer la forme d'onde du courant d'excitation (Fig . 30-40a). On constate qu'il est fortement distorsionné, atteignant une valeur crête de 14 A . Les pertes dans le fer sont données par l'expression

Pertes, rendement et capacité d'un transformateur

Comme toute machine électrique, le transformateur occasionne des pertes de puissance.

Ces pertes sont causées par: (voir Pertes, échauffement et rendement des machines électriques)

a) l'effet Joule dans les deux enroulements

b) l'hystérésis et les courants de Foucault dans le fer

Les pertes dans le transformateur se manifestent sous forme de chaleur et donnent lieu:

1) à une élévation de température

2) à une diminution de rendement Dans les conditions normales de fonctionnement, le rendement des transformateurs est très élevé ; il peut atteindre 99,5 % pour les transformateurs de grande puissance.

La quantité de chaleur occasionnée par les pertes dans le fer dépend de la valeur maximale θ_max du flux, laquelle dépend elle-même de la tension appliquée au primaire.

D'autre part, la puissance dissipée en chaleur dans les enroulements dépend de l'intensité du courant qui les parcourt.

Afin de maintenir la température du transformateur à une valeur acceptable, on est amené à limiter à la fois la tension qu'on lui applique et le courant qu'on en tire. C'est pour cette raison que la puissance nominale que peut débiter un transformateur est exprimée par le produit de la tension nominale et du courant nominal.

Cependant, le résultat n'est pas exprimé en watts, car l'angle entre la tension et le courant peut prendre n'importe quelle valeur, selon la nature de la charge.

Par conséquent, la puissance nominale est donnée en voltampères (VA), en kilovoltampères (kVA) ou en mégavoltampères (MVA). L'échauffement d'un transformateur dépend donc de la puissance apparente qui le traverse.

Ainsi, un transformateur de 500 kVA deviendra aussi chaud en alimentant une charge résistive de 500 kW qu'une charge capacitive de 500 kvar.

Les valeurs de la fréquence nominale, de la tension nominale et de l'intensité nominale des courants primaire et secondaire sont inscrites sur la plaque signalétique; ces valeurs ne doivent pas être dépassées sauf pour de courtes périodes.

Exemple 30-9

Un transformateur de 100 kVA a un rapport de transformation de 2400 à 600 volts

a) Quelles sont les intensités nominales des courants?

b) On applique une tension de 2000 volts seulement à l'enroulement haute tension du transformateur.

Peut-on en tirer 100 kVA sans risquer de le faire surchauffer?

Solution

a) Le courant nominal de l'enroulement de 2400 V est:

Le courant nominal de l'enroulement de 600 V est:

b) Il est vrai qu'en appliquant 2000 V seulement à l'enroulement haute tension on réduit le flux dans le noyau et, par suite, les pertes dans le fer; cependant, on ne doit pas tirer du transformateur un courant excédant sa valeur nominale.

La puissance maximale que l'on peut transformer sous cette tension réduite est donc:

S = 2000 V x 41,7 A = 83,4 kVA

Exemple 30-10

Un transformateur triphasé de 110 MVA, 222 kV à 34,5 kV, 60 Hz, possède les caractéristiques suivantes

masse du noyau (acier type M-14 jauge #29): 53,6 t

masse totale du cuivre : 15,2 t (1 t = 1000 kg)

densité (le flux dans le noyau : 1,4 T

densité de courant dans les enroulements : 2 A/mm²

Calculer:

a) les pertes dans le fer

b) les pertes dans le cuivre à 75 "C

c) le rendement du transformateur pour une charge de 110MW

d) le rendement pour une charge capacitive de 110 Mvar

Solution

a) En se référant aux courbes de la Fig. 29-5, Pertes, échauffement et rendement des machines électriques, on trouve: pertes massiques dans le fer à

B = 1,4 T : 2,6 W/kg

d'où les pertes totales dans le fer:

Pf= 2,6 x 53 600 = 139 360 W = 139 kW

b) En utilisant l'équation 29-1, on calcule les pertes Joule comme suit:

Résistivité du cuivre à 75 °C :

ρ = ρo (1 + αt) éq.10-2a

= 15,88 (1 + 0,00427 x 75) = 21,0 nΩm

Densité de courant = 2 A/mm² = 200 A/cm² d'où les pertes massiques dans le cuivre:

Les pertes totales dans les enroulements sont donc :

P_cu = 9,45 x 15 200 = 143 640 W = 144 kW

c) Les pertes totales sont:

P_f+ P_cu= 139 + 144 = 283 kW

La puissance active débitée par le transformateur est:

P₂ = 110 MW = 110 000 kW

La puissance active fournie au transformateur est:

P₁ = 110 000 + 283 = 110 283 kW

d'où le rendement:

d) Lorsque la charge est purement capacitive, la puissance active P₂ débitée par le transformateur est nulle. Cependant, la puissance active fournie au transformateur est toujours 283 kW.

Par conséquent:

 le rendement est nul.

Note: Les pertes supplémentaires engendrées dans les boulons, la cuve et dans les conducteurs de cuivre, à cause des flux de fuite, plus la puissance requise par les ventilateurs, peuvent augmenter de 10 % à 15 % les pertes totales calculées ci-dessus . Le rendement sera donc légèrement inférieur à celui que nous avons calculé.

Refroidissement des transformateurs

Si l'on veut empêcher qu'un échauffement exagéré détériore les isolants d'un transformateur, il faut en assurer un refroidissement convenable.

Dans les transformateurs de faible puissance et à basse tension, le refroidissement est assuré par la circulation naturelle de l'air environnant. L' enveloppe métallique de ces transformateurs est munie d'ouvertures permettant le libre passage de l'air (Fig. 30-4 1).

Figure 30-41 Transformateur monophasé de 25 kVA, 600 V/240 V, 60 Hz, isolation classe 150 °C, pour usage intérieur, refroidi par circulation naturelle de l'air. Hauteur; 600 mm ; largeur: 434 mm; profondeur: 230 mm; masse: 79,5 kg (Hammond).

Si l'on désire un refroidissement plus énergique, on peut souffler de l'air à l'intérieur de l'enveloppe métallique à l'aide d'un ventilateur.

Les transformateurs de distribution baignent dans une cuve contenant de l'huile minérale (Fig . 30-42).

Figure 30-42 Groupe de deux transformateurs monophasés à l'huile ayant une capacité de 75 kVA, 14,4 kV/240 V, 60 Hz, 55 °C, impédance = 4,2 %. Les petits radiateurs augmentent la surface de dissipation des cuves afin d'améliorer le refroidissement

L'huile assure le transport de la chaleur provenant du noyau et des enroulements jusqu'à la paroi de la cuve ; de là, la chaleur est ensuite cédée à l'air extérieur.

De plus, l'huile assure un isolement meilleur que l'air et elle protège les enroulements contre l'humidité de l'air.

L'humidité a pour effet d'accélérer l'oxydation des isolants soumis aux hautes tensions. La cuve est ordinairement refroidie par ventilation naturelle. La puissance des transformateurs de distribution est inférieure à 200 kVA.

Pour les grandes puissances, on augmente la surface de rayonnement de la cuve en disposant des radiateurs autour de celle-ci (Fig . 30-43).

Figure 30-43 Transformateur de mise à la terre de 1,9 MVA, 26,4 kV, 60Hz.

La capacité de ce transformateur est 25 fois plus grande que celle des transformateurs de la Fig . 30-42, mais il est encore refroidi par la circulation naturelle de l'air environnant. Remarquer toutefois que le radiateur est alors aussi volumineux que le transformateur lui-même.

L'huile s'échauffe dans le transformateur, monte dans la cuve et circule de haut en bas dans les tubes extérieurs où elle se refroidit.

Enfin, pour les transformateurs de plusieurs milliers de kVA, on facilite la dissipation de la chaleur en assurant la ventilation forcée des radiateurs eux-mêmes.

De puissants ventilateurs, disposés autour des radiateurs, produisent les courants d'air nécessaires (Fig . 30-44).

Figure 30-44 Transformateur triphasé de 1300 MVA, 24,5 kV/345 kV, 60 Hz . OFAF, 65 °C, impédance 11,5 %. Ce transformateur survolteur, installé à la centrale de génération nucléaire Cook à Bridgeman, Michigan, est un des plus gros jamais construits. Les pompes assurant la circulation d'huile sont visibles sous les ventilateurs (gracieuseté de Westinghouse).

Une autre méthode de refroidissement artificiel consiste à installer dans le bain d'huile un serpentin dans lequel circule un courant d'eau.

Certains transformateurs ont des capacités variables selon la méthode de refroidissement utilisée.

Par exemple, un gros transformateur (Fig. 30-45) peut avoir trois puissances nominales différentes de 36 000/48 000/ 60 000 kVA selon qu'il est refroidi:

Figure 30-45
Transformateur triphasé de 36/48/60 MVA, 225 kV/26,4 kV, ONAN/ONAF/OFAF, 60 Hz, impédance 7,4 % La capacité variable de cet appareil dépend du mode de refroidissement utilisé.

Le réservoir cylindrique permet l'expansion de l'huile lorsque la température augmente, tout en réduisant au minimum la surface de l'huile en contact avec l'air pour éviter l'oxydation .

Autres détails:

masse du noyau et des enroulements 37,7 t
masse de la cuve et les accessoires 28,6 t
masse de l'huile (44,8 m3) 38,2 t
masse totale 104,5 t

(a) par la convection naturelle de l'air (36 000 kVA).

(b) par la ventilation forcée avec des ventilateurs extérieurs (48 000 kVA),

ou (c) par la circulation forcée de l'huile au moyen de pompes, avec les ventilateurs en marche (60 000 kVA).

Ces méthodes de refroidissement élaborées restent économiques si l'on considère le coût élevé d'un gros transformateur dont le refroidissement serait assuré exclusivement par la circulation naturelle de l'air.

Le mode de refroidissement est désigné par les symboles suivants.

AA.transformateur à sec, circulation naturelle de l'air

AFA.transformateur à sec, circulation forcée de l'air

OA .transformateur à l'huile*, circulation naturelle de l'air

OA/FA-transformateur à l'huile, circulation naturelle de l'air / circulation forcée de l'air

OA/FA/FOA .transformateur à l'huile, circulation naturelle de l'air / circulation forcée de l'air / circulation forcée de l'huile et de l'air.

Les désignations suivantes sont aussi employées:

ONAN .circulation naturelle de l'huile (ON) et de l'air (AN)

ONAF-circulation forcée de l'air (AF)

La lettre «O» désigne l'huile («oil»).

OFAF.circulation forcée de l'huile (OF) et de l'air (AF)

L'échauffement par résistance admis pour les transformateurs à l'huile est soit 55 °C soit 65 °C.

 On doit limiter l'échauffement à des valeurs basses pour em.pêcher la détérioration rapide de l'huile.

Par contre, l'échauffement des transformateurs à sec peut s'élever jusqu'à que 180 °C, selon le type d'isolant utilisé.

Application du système p.u. aux transformateurs

Nous avons à la section Notions de mécanique les principes d'utilisation du système de mesure relative, ou le système «per unit» (p.u.).

Dans le cas des transformateurs, on choisit deux grandeurs de base, soit la puissance nominale S_n et la tension nominale E_n du transformateur. Il s'ensuit que le courant de base et l'impédance de base sont respectivement

I_n = S_n / E_n et Z_n = E_n / I_n

Noter que E_n et I_n sont les valeurs nominales du côté primaire ou du côté secondaire.

On peut aussi calculer l'impédance de base par la formule suivante :

Z_n = E²_n / S_n

où

Z_n = impédance de base du transformateur [Ω]

S_n = puissance nominale du transformateur [VA]

E_n = tension nominale du primaire ou du secondaire [V]

Comme les tensions primaire et secondaire sont habituellement différentes, le transformateur possède deux impédances de base: l'une pour le primaire, l'autre pour le secondaire.

Nous les désignons respectivement par les symboles Z_np et Z_ns.

Exemple 30-11

Calculer les impédances (le base au primaire et au secondaire d'un transformateur de 250 kVA, 4160 V/480 V. 60 Hz.

Solution

Impédance de base au primaire:

Impédance de base au secondaire:

Impédances d'un transformateur exprimées en p.u.

Il est particulièrement utile, pour fins de comparaison, de connaître la valeur relative des diverses impédances (résistances, réactances de fuite, etc.) d'un transformateur.

Par définition, ces impédances en p.u. sont calculées en faisant le rapport entre la valeur réelle de l'impédance en ohms et l'impédance de base (Z_np ou Z_ns) correspondant à l'enroulement considéré .

On donne au tableau 30-1 les valeurs typiques en p .u. pour des transformateurs ayant une capacité comprise entre 3 kVA et 100 MVA.

On remarque que pour un paramètre donné (R₁ ou X_m, par exemple), la valeur en p.u. demeure du même ordre de grandeur, quelles que soient la puissance et les tensions primaire et secondaire.

Cette constatation est surprenante, surtout si l'on considère qu'il existe une différence de taille aussi grande entre deux transformateurs de 3 kVA et 100 MVA qu'entre une mouche et un éléphant!

Exemple 30-12

En utilisant l'information donnés au tableau 30-1, calculer l'ordre de grandeur des impédances d'un transformateur de 250 kVA. 4160V/480V, 60 Hz.

Solution

Calculons d'abord les impédances de base du primaire et du secondaire.

D'après les valeurs trouvées à l'exemple 30-11, on a:

Z_np = 69 Ω    Z_ns = 0,92 Ω

Calculons les valeurs réelles des impédances respectives en multipliant Z_np et Z_ns par les valeurs en p.u. fournies dans le tableau 30-1.

On obtient:

Le circuit équivalent de ce transformateur est donné à la Fig. 30-46.

Figure 30-46 Circuit équivalent d'un transformateur de 250 kVA, 4160 V/480 V, 60 Hz (voir exemple 30-12)

Les valeurs réelles peuvent être situées dans une plage comprise entre 50 % et 200 % des va.leurs calculées plus haut, car les valeurs fournies dans le tableau 30-1 sont approximatives.

L'impédance d'un transformateur est habituellement exprimée en pour cent de l'impédance de base du primaire ou du secondaire. Le pourcentage d'impédance est toujours inscrit sur la plaque signalétique.

Les impédances en p.u. et en pour cent sont liées par la relation:

Z_% = Z_pu X 100    (30-18)

Exemple 30-13

Un transformateur de 3000 kVA, 69 kV/4,16 kV, 60 Hz possède une impédance de 8%.

Calculer:

a) la valeur de l'impédance rapportée au primaire

b) la régulation de tension pour une charge résistive de. 2000 kW

c) la valeur des courants si un court-circuit se produit au secondaire, la tension au primaire demeurant égale à 69 kV

Solution

a) L'impédance de base du primaire est:

Figure 30-47 Voir exemple 30-13.

Solution

a) L'impédance de base du primaire est:

De l'expression (30-18) on tire :

Z_% = Z_pu X 100

8 = Z_pu x 100

donc Z_pu = 8 / 100 = 0,08

L'impédance totale du transformateur rapportée au primaire est donc :

Z_p = Z_pu x Z_np = 0,08 x 1587 Ω = 127 Ω

Comme la puissance du transformateur excède 250 kVA, la résistance des enroulements est négligeable comparée à la réactance de fuite.

On peut donc écrire:

Z_p = X_p = 127Ω

Voir la Fig. 30-47a.

b) L'impédance correspondant à une charge de 2000 kW au secondaire est:

Le rapport de transformation est :

La valeur de Z rapportée au primaire est:

En se référant au circuit de la Fig. 30-47b, on obtient:

Il s'ensuit que:

d'où la tension E, sous charge:

À vide, la tension au secondaire est 4160 V

La régulation de tension, en pour cent, est définie par :

La régulation est donc excellente.

c) Si un court-circuit se produit aux bornes du secondaire, le courant au primaire devient:

Le courant correspondant au secondaire est:

Un calcul rapide indique que les courants de court-circuit au primaire et au secondaire sont 12,5 fois plus grands que les courants nominaux de ces deux enroulements.

Les pertes Joule sont donc 12,5 2 = 156 fois supérieures aux pertes à pleine charge. Le disjoncteur ou fusible protégeant le transformateur doit s'ouvrir très rapidement afin d'empêcher un échauffement excessif.

Ces courants intenses produisent aussi des forces électromagnétiques très fortes.

Celles-ci sont également 156 fois plus grandes que normal, c'est pourquoi les enroulements doivent être solidement attachés (voir section Forces électromagnétiques) .

Mesure des impédances d'un transformateur

On peut déterminer la valeur des impédances d'un transformateur au moyen d'un essai à vide et d'un essai en court-circuit.

1 . Essai à vide.

Lors de l'essai à vide, la tension nominale est appliquée à un des enroulements (disons le primaire) et les valeurs de E_p, E_s , I_o, et de la puissance active P_m sont mesurées (Fig. 30-48).

Figure 30-48 Essai à vide et détermination de R_m, X_m et du rapport de transformation a

Lors d'un essai à vide, les pertes Joule dans l'enroulement alimenté sont toujours négligeables.

On peut donc écrire:

1 . Puissance apparente absorbée par le noyau:

S_m = E_p x I_o

2. Puissance réactive absorbée par le noyau :

3. Valeur de R_m :

     eq. 30-12

4. Valeur de X_m:

    eq. 30-13

5. Rapport de transformation

2. Essai en court-circuit.

Lors de l'essai en court-circuit, un des enroulements est mis en court-circuit (disons le secondaire) et une tension E, beaucoup plus petite que la tension nominale, est appliquée au primaire.

Afin d'éviter de surchauffer les enroulements, la tension est augmentée graduellement de façon à obtenir un courant n'excédant pas le courant nominal.

On mesure alors E_c, I_c et la puissance active P_c (Fig. 30-49).

Figure 30-49 Essai en court-circuit et détermination de R_p, X_p et Z_p

Ces lectures donnent l'information suivante :

6. Impédance totale du transformateur rapportée au primaire:

Z_p = E_c / I_c

7. Résistance totale du transformateur rapportée au primaire:

R_p = P_c / I²_c

8. Réactance de fuite totale du transformateur rapportée au primaire:

On peut aussi déterminer la valeur de R_p en mesurant les résistances R₁ et R₂ des enroulements primaire et secondaire.

On a alors R_p = R₁ + a²R₂.

Exemple 30-14

Soit un transformateur de 500 kVA, 69 kV/4160 V, 60 Hz.

Lors d'un essai en court-circuit, les bornes X₁, X₂ étant reliées, on a relevé les lectures suivantes:

E 2600 V = 2400 W

Calculer du côté HT:

a) l'impédance totale du transformateur

b) la résistance totale du transformateur

c) la réactance de fuite totale du transformateur

d) le pourcentage d'impédance

Calculer ensuite:

e) l'impédance rapportée au côté BT

f) le pourcentage d'impédance rapporté au côté BT

Solution

a) Impédance du transformateur vue du côté HT:

b) Résistance du transformateur vue du côté HT:

c) Réactance de fuite vue du côté HT :

d) Impédance de base du côté HT:

d'où l'impédance relative vue du côté HT:

et le pourcentage d'impédance :

e) Impédance du transformateur vue du côté BT :

f) Impédance de base du côté BT :

Pourcentage d'impédance vue du côté BT:

Exemple 30-15

Un essai à vide sur le transformateur de 500 kVA, 69 kV/4160V, décrit à l'exemple 30-14 donne les résultats suivants lorsque l'enroulement BT est excité:

E_s =4160V     I_o = 2.4A     P_m=2100W

Calculer:

a) les valeurs de R_m vues du côté BT et HT

b) les valeurs de X_m vues du côté BT et HT

Tracer le circuit équivalent du transformateur.

Solution

a) Valeur de R_m vue du côté BT:

Valeur de R_m vue du côté HT:

b) Valeur de I_f vue du côté BT:

Valeur de I_m vue du côté BT:

Valeur de X_m vue du côté BT:

Valeur de X_m rapportée au côté HT:

Le circuit équivalent du transformateur est montré à la Fig. 30-50.

Figure 30-50 Circuit équivalent d'un transformateur obtenu à partir des essais à vide et en court-circuit (voir exemples 30-14 et 30-15)

Les bornes accessibles sont H₁, H₂, X₁ et X₂. Selon que le transformateur fonctionne à vide ou en charge, ce circuit équivalent peut être simplifié comme expliqué à la section 30.15 .

Transformateurs en parallèle

Il est parfois nécessaire de brancher deux transformateurs en parallèle. C'est le cas, par exemple, lorsque la charge dépasse la puissance nominale d'un seul transformateur.

Pour que deux transformateurs puissent fonctionner en parallèle, il faut d'abord que les deux aient le même rapport de transformation.

De plus, il faut joindre les bornes de même polarité comme l'indique la Fig. 30-51.

Figure 30-51 Méthode de raccordement de deux transformateurs en parallèle

Si l'on se trompe dans les connexions, l'équivalent d'un court-circuit franc est créé aux bornes de la source alimentant les deux transformateurs.

Afin de calculer les courants circulant dans chaque transformateur, on doit déterminer le circuit équivalent des deux transformateurs en parallèle.

Considérons d'abord le circuit équivalent d'un seul transformateur alimentant une charge Z_L (Fig. 30-52a).

Figure 30-52a Circuit équivalent d'un transformateur alimentant une charge ZL

La tension au primaire est E_p, et l'impédance du transformateur rapportée au primaire est Z_p1.

Le rapport de transformation étant a, le circuit peut être simplifié comme indiqué à la Fig. 30-52b.

Figure 30-52b Circuit équivalent où toutes les impédances sont rapportées au côté primaire

Lorsqu'un deuxième transformateur d'impédance Z_p2 est branché en parallèle avec le premier, le circuit équivalent prend la forme indiquée à la Fig. 30-53.

Figure 30-53 Circuit équivalent de deux transformateurs en parallèle, alimentant une charge ZL. Toutes les impédances sont rapportées au côté primaire

On constate que les impédances Z_p1 et Z_p2 sont en parallèle et que le courant I de la charge se divise en deux parties, I₁ et I₂ circulant dans les deux transformateurs.

Étant donné que la chute de tension E₁₃ est la même pour

chaque impédance, on peut écrire:

I₁Z_p1 = I₂Z_p2

soit

I₁ / I₂ = Z_p2 / Z_p1  (30-19) 

Le rapport des courants dépend donc du rapport des impédances.

Cependant, pour que l'échauffement soit le même pour chaque transformateur, les courants doivent être proportionnels aux puissances nominales respectives, d'où la relation :

I₁ / I₂ = S_n1 / S_n2  (30-20)

En combinant les équations 30-17, 30-19 et 30-20, on peut prouver que les transformateurs peuvent fournir chacun leur puissance nominale pour autant qu'ils possèdent le même pourcentage d'impédance.

Dans le cas contraire, la capacité totale disponible est inférieure à la somme des puissances nominales des deux transformateurs. Ce point est illustré par l'exemple suivant.

Exemple 30-16

Un transformateur de 100 kVA avant une impédance de 4% est connecté en parallèle avec un autre transformateur de 250 kVA dont l'impédance est de 6% (Fig. 30-54). Le rapport (le transformation est de 7200V/240 V et la charge est de 330 KVA.

Figure 30-54 Raccordement des transformateurs (voir exemple 30-16)

Calculer:

a) le courant nominal au primaire de chaque transformateur

b) l'impédance de la charge rapportée au primaire

c) l'impédance de chaque transformateur rapportée au primaire

d) le courant réel circulant dans le primaire de chaque transformateur

Solution

a) Courant nominal au primaire du transformateur de 250 kVA:

I_n1 = 250 kVA / 7200 V = 34,7 A

Courant nominal au primaire du transformateur de 100 kVA:

I_n2 = 100 kVA / 7200 V = 13,9 A

b) Impédance de la charge rapportée au primaire :

c) Impédance de base du transformateur de 250 kVA rapportée au primaire:

Impédance du transformateur de 250 kVA rapportée au primaire:

Z_p1 = Z_1(P.u) X Z_np1 = 0,06 x 207Ω = 12,4Ω

Impédance de base du transformateur de 100 kVA rapportée au primaire:

Z_np2 = E²_p / S_n2 = 7200² / 100 000 = 518Ω

L'impédance du transformateur de 100 kVA rapportée au primaire est:

Z_p2 = 0,04 X 518Ω = 20,7Ω

d) Le circuit équivalent des deux transformateurs et de la charge est montré à la Fig. 30-55.

Figure 30-55 Circuit équivalent du montage de la Fig. 30-54 (voir exemple 30-16)

Le courant dans la charge est:

I₁ = S_charge / E_p = 330 000 / 7200 = 46 A

Le courant I₁ porté par le transformateur de 250 kVA est:

I₁ = 46 A x (20,7Ω / (20,7Ω + 12,4Ω) = 28,8 A

Le courant Il porté par le transformateur de 100 kVA est:

I₂ = 46A .28,8A = 17,2A

Le transformateur de 100 kVA est surchargé du fait qu'il porte un courant de 17,2 A alors que son courant nominal est seulement de 13,9 A.

Cela représente une surcharge de 24 %.

Par contre, le transformateur de 250 kVA n'est pas surchargé car il porte un courant de 28,8 A alors que son courant nominal est de 34,7 A.

Les transformateurs ne se partagent pas la charge en proportion de leur puissance nominale parce que leurs pourcentages d'impédance n'ont pas les mêmes valeurs. Le transformateur ayant le plus faible pourcentage d'impédance accapare une plus forte proportion de la charge.

Notons que dans cet exemple, si les deux transformateurs avaient le même pourcentage d'impédance, ils pourraient alimenter une charge de 250 + 100 = 350 kVA, sans surchauffer alors qu'ils ne peuvent même pas porter une charge de 330 kVA.

 Résumé

Le transformateur est un appareil très simple permettant de modifier la tension et le courant dans un circuit à courant alternatif.

Dans sa forme la plus élémentaire, il est constitué de deux bobines couplées appelées primaire (côté source) et secondaire (côté charge) montées sur un noyau. Bien que le transformateur idéal n'existe pas, il est important d'en connaître les propriétés fondamentales car les transformateurs utilisés en pratique ont des propriétés très semblables.

Pour le transformateur idéal, le rapport des tensions primaire et secondaire est égal au rapport des nombres de tours de ces deux enroulements. Les courants sont dans le rapport inverse.

Le transformateur idéal change donc les valeurs des tensions et des courants, et «transforme» les impédances. Toutefois, la puissance active et la paissance réactive sont transportées sans aucune perte du primaire au secondaire.

Pour les transformateurs utilisés en pratique, il faut considérer les pertes et le couplage imparfait entre les bobines. Le noyau de fer est le siège de pertes actives dues à l'hystérésis et aux courants de Foucault.

De plus, le flux requis par le noyau exige un courant magnétisant qui se traduit par une absorption de puisssance réactive. À cause de la résistance des enroulements, des pertes sont également dissipées dans le cuivre.

Enfin, comme tout le flux créé par le primaire ne traverse pas complètement le secondaire, et vice versa, il faut considérer les flux de fuite qui se traduisent par des puissances réactives supplémentaires.

L'échauffement causé par les pertes actives dissipées dans le noyau et les enroulements exigent l'utilisation de méthodes de refroidissement. Selon la puissance, on utilise le refroidissement par circulation naturelle ou forcée de l'air et/ou de l'huile.

Malgré leurs imperfections, les transformateurs demeurent des appareils de rendement élevé.

Si l'on prend en considération les différentes imperfections du transformateur, on peut établir un circuit équivalent pour le transformateur réel.

Ce circuit comprend un transformateur idéal auquel on ajoute les résistances et les réactances de fuite des enroulements, ainsi qu'une branche de magnétisation. Ce circuit permet de calculer avec précision les pertes et les chutes de tension à l'intérieur du transformateur.

Dans les calculs impliquant des transformateurs de grande puissance, on peut même simplifier le circuit équivalent à une simple réactance de fuite en série avec le transformateur idéal.

PROBLÈMES

Niveau pratique

30-1 Quelles sont les parties essentielles d'un transformateur?

30-2

a) À quoi sert le courant tiré par un transformateur fonctionnant à vide?

b) Peut-on le négliger dans les calculs pratiques lors.que le transformateur est en charge?

 30-3 Expliquer comment une tension est induite au secondaire d'un transformateur. Que veut dire flux mutuel? flux de fuite?

30-4 Si le secondaire d'un transformateur possède deux fois plus de spires que le primaire, la tension secondaire est-elle plus faible que la tension primaire?

30-5 Quelles sont les relations entre les tensions et les courants au primaire et au secondaire d'un transformateur idéal en charge?

30-6 Nommer les sources de pertes dans un transformateur.

30-7 Quel enroulement alimente la charge : le primaire ou le secondaire?

30-8 Nommer deux conditions essentielles pour brancher deux transformateurs en parallèle .

30-9 À quoi servent les prises de réglage des transformateurs?

30-10 Nommer trois modes de refroidissement des transformateurs. Comment les désigne-t-on?

30-11 Une tension de 600 V est appliquée au primaire d'un transformateur possédant 1200 spires au primaire et 240 spires au secondaire. Calculer la valeur de la tension secondaire.

30-12 On branche l'enroulement basse tension d'un transformateur à une source de tension de 2400 V.

Quelle tension recueille-t-on sur l'enroulement haute tension sachant que les enroulements haute tension et basse tension possèdent respectivement 7500 spires et 300 spires.

30-13 Une ligne de distribution alimente sous une tension de 6900 V un transformateur dont le primaire comporte 1500 spires et le secondaire 24 spires.

Calculer:

a) la tension secondaire

b) les courants primaire et secondaire si une charge de 5Ω est raccordée au secondaire

30-14 L'enroulement primaire d'un transformateur possède deux fois plus de spires que le secondaire. La tension primaire est de 220 V. Le secondaire est raccordé à une résistance de 5Ω.

Calculer la puissance débitée par le transformateur ainsi que les courants primaire et secondaire.

30-15 Un transformateur de 3000 kVA a un rapport de transformation de 60 kV à 2,4 kV. Calculer le courant nominal de chaque enroulement.

30-16 La bobine de la Fig. 30-2 possède 500 spires de résistance négligeable, et sa réactance est de 60Ω. Elle est raccordée à une source de 120 V, 60 Hz .

Calculer:

a) la valeur efficace du courant I_m

b) la valeur crête de I_m

c) la valeur crête de la FMM développée par la bobine

d) la valeur crête du flux Φ

30-17 Dans le problème 30-16, calculer la nouvelle valeur de la FMM et du flux crête si la tension de la source est réduite à 40 V.

30-18 On donne l'information suivante relative me au transformateur idéal illustré à la Fig. 30-8:

N₁ = 500 spires     E_g = 600 V     N₂ = 300 spires     Z = 12Ω (résistif)

Calculer la valeur de:

a) E₂ I₂ I₁

b) la puissance fournie au primaire

c) la puissance débitée par le secondaire

d) l'impédance vue par la source Niveau intermédiaire

30-19 Dans le problème 30-11, calculer la valeur maximale du flux dans le noyau si la fréquence est de 60 Hz.

30-20 Expliquer pourquoi le flux maximal dans un transformateur doit demeurer constant lorsque la tension d'alimentation reste constante?

30-21 Surie schéma de la Fig. 30-4, le primaire elle secondaire possèdent respectivement 200 spires et 600 spires. La tension d'alimentation a une valeur efficace de 120 V, 60 Hz; le courant magnétisant I_m est de 3 A.

On constate que 40 % du flux Φ créé par le primaire est accroché par le secondaire.

Calculer:

a) la valeur efficace de la tension E₂

b) la valeur crête du flux Φ

c) Tracer le diagramme vectoriel montrant les vecteurs E_g, I_m, E₂, Φ_m1 et Φ_f1

30-22 Dans la Fig. 30-36a, on applique une tension de 600 V aux bornes H₁ H₂ et l'on mesure une tension de 80 V entre les bornes X₁ et X₂.

a) Quelle tension mesure-t-on entre les bornes H₁ et X₂?

b) Quelle tension mesure-t-on entre les bornes H₂ X₂ si l'on relie les bornes H₁ X₁ ?

30-23

a) Qu'arriverait-il si, dans la Fig.30-51, on intervertissait les connexions aux bornes H₁ et H₂ du transformateur B?

b) Le fonctionnement du groupe serait-il affecté si l'on intervertissait les bornes H₁ H₂ et les bornes X₁ X₂ du transformateur B?

Expliquer.

30-24 Expliquer pourquoi la tension au secondaire d'un transformateur diminue à mesure que la charge résistive augmente?

30-25 Qu'entend-on par:

a) impédance d'un transformateur?

b) pourcentage d'impédance d'un transformateur?

30-26 Un transformateur de 3000 kVA ayant un rapport de transformation de 60 kV à 24 kV a une impédance de 6 %. Quelle est la valeur de l'impédance (en ohms) ramenée:

a) au primaire de 60 kV?

b) au secondaire de 2,4 kV?

c) Sachant que la tension au primaire est de 67,5 kV, calculer la valeur des courants dans chaque enroulement lors d'un court-circuit au secondaire.

30-27 On applique une tension de 2300 V entre les bornes 1 et 4 du transformateur montré à la Fig.30-39.

a) Quelle est la tension entre les bornes X₁ X₂?

b) Calculer la valeur des courants dans chaque enroulement lorsque l'on applique une charge de 12 kVA au secondaire.

30-28 Un transformateur de 66,7 MVA a un rendement de 99,3 % lorsqu'il alimente une charge dont le facteur de puissance est de 100 %.

a) Calculer les pertes, en kilowatts dans ces circonstances.

b) Calculer les pertes et le rendement de ce transformateur lorsqu'il alimente une charge de 66,7 MVA dont le facteur de puissance est de 80 %.

30-29 Le transformateur de la Fig. 30-45 alimente une charge de 44 MVA.

Quel mode de refroidissement doit-on utiliser pour que l'on obtienne le rendement maximal sans dépasser l'échauffement permis?

30-30 Si l'on vidait l'huile du transformateur de la Fig. 30-42, sa capacité baisserait de 75 kVA à 40 kVA. Expliquer.

30-31 Si l'on plaçait le transformateur de la Fig. 30.41 dans une cuve remplie d'huile, la température maximale de 150 °C devrait être abaissée à 95 °C.

Expliquer.

Niveau avancé

30-32 Un transformateur idéal ayant 300 spires au primaire et 1200 spires au secondaire est alimenté par une source de 600 V.

La charge résistive est de 100Ω. Calculer la valeur maximale du flux dans le noyau sa.chant que la fréquence de la source est de 50 Hz.

30-33 Plus les flux de fuite d'un transformateur sont importants, plus son impédance est élevée. Expliquer.

30-34 Pour le transformateur de la Fig. 30-25, on fournit les renseignements suivants :

R₁ = 18Ω     R₂ = 0,005Ω     X_f1 = 40Ω     X_f2 = 0.01Ω     E₁ = 14,4 kV     E₂ = 240 V

La capacité du transformateur est de 75 kVA. En négligeant la branche d'excitation,

calculer :

a) l'impédance du transformateur ramenée au primaire (14,4 kV)

b) le pourcentage d'impédance du transformateur vu du côté primaire

c) l'impédance du transformateur ramenée au secondaire (240 V)

d) le pourcentage d'impédance vu du côté secondaire

e) les pertes totales dans le cuivre à pleine charge

f) les valeurs en p.u. de la résistance et de la réactance du transformateur

30-35 Pour déterminer l'impédance d'un transformateur monophasé de 10MVA, 66 kV/7,2 kV, on utilise le montage de la Fig. 30-49. On mesure les valeurs suivantes :

E_c=2640V     I_c =72A      P_c =9,85 kW

Calculer:

a) la résistance et la réactance de fuite rapportées au primaire

b) l'impédance de base du côté primaire

c) le pourcentage d'impédance du transformateur

30-36 Dans le problème 30-35, les pertes dans le fer sont de 35 kW.

Calculer le rendement du transformateur à pleine charge à un FP de 100 %.

30-37 En se basant sur les données du transformateur de la Fig. 30-45, faire une estimation de la puissance du transformateur de la Fig. 30-44 en supposant que l'on arrête les ventilateurs et les pompes de circulation d'huile.

30-38 Un transformateur construit selon le schéma de la Fig. 30-21 aurait une très mauvaise régulation.

Expliquer pourquoi et comment l'améliorer.

Réponses

11) 120 V; 12) 60 kV; 13a) 110,4 V; 13b) 22,1 A; 13c) 0,353 A;
14) 2420 W; 11 A; 22 A; 15) 50 A; 1250 A; 16a) 2 A; 16b) 2,83 A;
16c) 1414 A; 16d) 0,90 mWb; 17) 471,3 A; 0,3 mWb;
18a) 360 V; 30 A; 18 A; 18b) 10,8 kW; 18c) 10,8 kW; 18d) 33,3Ω;
19) 1,88 mWb; 21 a) 144 V; 21b) 2,25 mWb; 22a) 0 V; 22b) 520 V;
26a) 72Ω; 26b) 0,1152Ω; 26c) 937,5 A; 23,4 kA; 27a) 126,4 V;
27b) 5,22 A; 94,9 A; 28a) 470 kW; 28b) 470 kW; 99,1 %;
29) ONAF; 32) 9 mWb; 34a) 84,1Ω; 34b) 3%; 34c) 0,0234Ω;
34d) 3%; 34e) 977 W; 34f) R = 0,013 p.u.; X = 0,0275 p.u. ;
35a) 1,9Ω; 36,6Ω; 35b) 435,6Ω; 35c) 8,42%; 36) 99,2%;
37) 780 MVA